题目内容
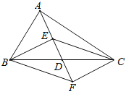
【题目】如图,已知![]() 和
和![]() 是两个边长都为
是两个边长都为![]() 的等边三角形,且点
的等边三角形,且点![]() ,
,![]() ,
,![]() ,
,![]() 在同一直线上,连接
在同一直线上,连接![]() ,
,![]() .
.
![]() 求证:四边形
求证:四边形![]() 是平行四边形;
是平行四边形;
![]() 若
若![]() 沿着
沿着![]() 的方向匀速运动,
的方向匀速运动,![]() 不动,当
不动,当![]() 运动到点
运动到点![]() 与点
与点![]() 重合时,四边形
重合时,四边形![]() 是什么特殊的四边形?说明理由.
是什么特殊的四边形?说明理由.

【答案】(1)证明见解析;(2)四边形![]() 是矩形;理由见解析;
是矩形;理由见解析;
【解析】
1、根据△ABC与△DEF是边长为8的等边三角形,可知∠1=∠2=60°,DE=AC,可得DE∥AC,所以四边形AEDC是平行四边形.
2、因为移动△ABC后点B与点F重合,平行四边形AEDC的对角线相等,根据矩形的判定,就可证明四边形AEDC是矩形.
![]() ∵
∵![]() 与
与![]() 是边长为
是边长为![]() 的等边三角形,
的等边三角形,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .
.
∴四边形![]() 是平行四边形.
是平行四边形.

![]() 四边形
四边形![]() 是矩形,理由如下:
是矩形,理由如下:

∵点![]() 与点
与点![]() 重合,
重合,
∴![]() ,
,![]() .
.
∴![]() .
.
由![]() 可知四边形
可知四边形![]() 是平行四边形,
是平行四边形,
∴四边形![]() 是矩形.
是矩形.

练习册系列答案
相关题目