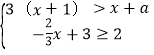题目内容
【题目】如图，在四边形
中，
、
为对角线，点
、
、
、
分别为
、
、
、
边的中点，下列说法：
①当
时，、、、四点共圆．②当
时，、、、四点共圆．③当且时，、、、四点共圆．其中正确的是（ ）
A. ①② B. ①③ C. ②③ D. ①②③
【答案】C
【解析】
连接EM,MF,FN,NE,连接EF,MN,交于O,利用三角形中位线定理可证明四边形ENFM为平行四边形，然后根据判定出ENFM的形状，可知M,E,N,F是否共圆.
连接EM,ME,FN,NE,FE,NM,交于点O，
∵M,E,N,F为AD,AB,CB,CD的中点，
∴EM∥BD∥NF，EN∥AC∥ME,EM=NF=
BD,EN=MF=AC,
∴四边形ENFM为平行四边形.
当AC=BD,则有EM=EN,所以平行四边形ENFM是菱形，而菱形的四个顶点不一定共圆，故①不一定成立,
当AC⊥BD时，由EMBD,EN∥AC，EM∥EN,可得：∠MEN=90°，所以平行四边形ENFM为矩形，则有OE=ON=OF=OM,所以E,M,N,F四点共圆，正确
当AC=BD且AC⊥BD，同理可得四边形ENFM为正方向，则有OE=ON=OF=OM,所以MENF四点共圆，正确，
所以答案选择C项.
练习册系列答案
相关题目
