题目内容
4. 如图,△P1OA1,△P2A1A2都是等腰直角三角形,点P1,P2都在函数y=$\frac{4}{x}$(x>0)的图象上,斜边OA1、A1A2都在x轴上,则点P2的坐标是( )
如图,△P1OA1,△P2A1A2都是等腰直角三角形,点P1,P2都在函数y=$\frac{4}{x}$(x>0)的图象上,斜边OA1、A1A2都在x轴上,则点P2的坐标是( )| A. | (4$\sqrt{2}$,$\sqrt{2}$) | B. | (4+2$\sqrt{2}$,4-2$\sqrt{2}$) | C. | (2+2$\sqrt{2}$,2$\sqrt{2}$-2) | D. | (4+2$\sqrt{2}$,2+2$\sqrt{2}$) |
分析 过点P1作P1B⊥x轴,垂足为B,△P1OA1是等腰直角三角形,所以X1=Y1.P1(x1,y1)在函数y=$\frac{4}{x}$(x>0)的图象上,x1=y1=2,即P1B=OB=2,△P1OA1是等腰直角三角形,推出OA1=4.过点P2作P2C⊥x轴,垂足为C,△P2A1A2,△P3A2A3都是等腰直角三角形,所以A1C=P2C=Y2,OC=OA1+A1C=4+y2=x2,P2(x2,y2),在函数y=$\frac{4}{x}$(x>0)的图象上,所以y2=$\frac{4}{{x}_{2}}$,解得y2=2$\sqrt{2}$-2,x2=2+2$\sqrt{2}$,据此可得出结论.
解答 解:过点P1作P1B⊥x轴,垂足为B,△P1OA1是等腰直角三角形,
∴x1=y1.
∵P1(x1,y1)在函数y=$\frac{4}{x}$(x>0)的图象上,x1=y1=2,即P1B=OB=2,
∴△P1OA1是等腰直角三角形,
∴OA1=4.
过点P2作P2C⊥x轴,垂足为C,△P2A1A2,△P3A2A3都是等腰直角三角形,
∴A1C=P2C=y2,OC=OA1+A1C=4+y2=x2,
∵P2(x2,y2)在函数y=$\frac{4}{x}$(x>0)的图象上,
∴y2=$\frac{4}{{x}_{2}}$,
解得y2=2$\sqrt{2}$-2,x2=2+2$\sqrt{2}$,
∴P2的坐标是(2+2$\sqrt{2}$,2$\sqrt{2}$-2).
故选C.
点评 考查反比例函数图象上点的坐标特点与等腰直角三角形的性质等知识.巧妙借助反比例函数图象性质与等腰直角三角形的性质相结合,综合性很强.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.下列运算正确的是( )
| A. | 2a2•a3=2a6 | B. | (3ab)2=6a2b2 | C. | 2abc+ab=2 | D. | 3a2b+ba2=4a2b |
15.下列说法正确的是( )
| A. | 一个游戏的中奖概率是$\frac{1}{10}$,则做10次这样的游戏一定会中奖 | |
| B. | 一组数据6,8,7,8,8,9,10的众数和中位数都是8 | |
| C. | 为了解全国中学生的心理健康情况,应该采用普查的方式 | |
| D. | 若甲组数据的方差S2甲=0.01,乙组数据的方差S2乙=0.1,则乙组数据比甲组数据稳定 |
12.数轴上点A表示a,将点A沿数轴向左移动3个单位得到点B,设点B所表示的数为x,则x可以表示为( )
| A. | a-3 | B. | a+3 | C. | 3-a | D. | 3a+3 |
19.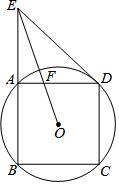 如图,边长为2的正方形ABCD内接于⊙O,过点D作⊙O的切线交BA延长线于点E,连接EO,交AD于点F,则EF长为( )
如图,边长为2的正方形ABCD内接于⊙O,过点D作⊙O的切线交BA延长线于点E,连接EO,交AD于点F,则EF长为( )
 如图,边长为2的正方形ABCD内接于⊙O,过点D作⊙O的切线交BA延长线于点E,连接EO,交AD于点F,则EF长为( )
如图,边长为2的正方形ABCD内接于⊙O,过点D作⊙O的切线交BA延长线于点E,连接EO,交AD于点F,则EF长为( )| A. | $\frac{\sqrt{6}}{3}$ | B. | $\frac{2\sqrt{6}}{3}$ | C. | $\frac{\sqrt{10}}{3}$ | D. | $\frac{2\sqrt{10}}{3}$ |
9.某市预计2022年初中毕业生学业考试10门学科整合后的满分值如下表:
请问根据130,120,100,150,120,40中,众数、中位数分别是( )
| 科目 | 语文 | 数学 | 英语 | 理化生 | 政史地 | 体育 |
| 满分值 | 130 | 120 | 100 | 120 | 120 | 40 |
| A. | 150,120 | B. | 120,120 | C. | 130,120 | D. | 120,100 |
13.全球海洋总面积约为36105.9万平方公里,用科学记数法表示为( )
| A. | 3.61×108平方公里 | B. | 3.60×108平方公里 | ||
| C. | 361×106平方公里 | D. | 36100万平方公里 |
 用5个完全相同的小正方体组合成如图所示的立体图形,它的俯视图是( )
用5个完全相同的小正方体组合成如图所示的立体图形,它的俯视图是( )



 如图所示,反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象经过矩形OABC的对角线AC的中点D.若矩形OABC的面积为8,则k的值( )
如图所示,反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象经过矩形OABC的对角线AC的中点D.若矩形OABC的面积为8,则k的值( )