题目内容
19.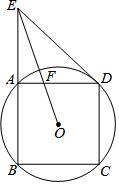 如图,边长为2的正方形ABCD内接于⊙O,过点D作⊙O的切线交BA延长线于点E,连接EO,交AD于点F,则EF长为( )
如图,边长为2的正方形ABCD内接于⊙O,过点D作⊙O的切线交BA延长线于点E,连接EO,交AD于点F,则EF长为( )| A. | $\frac{\sqrt{6}}{3}$ | B. | $\frac{2\sqrt{6}}{3}$ | C. | $\frac{\sqrt{10}}{3}$ | D. | $\frac{2\sqrt{10}}{3}$ |
分析 由切线以及正方形的性质证明AE=AD=2,勾股定理可求得OE,根据平行线分线段成比例定理可证得EF=2OF,则EF=$\frac{2}{3}$OE,由此即可解决问题.
解答 解:如图2,作OM⊥AB于M,
∵AD是⊙O的切线,
∴∠EDO=90°,
∵O为正方形的中心,
∴M为AB中点,∠ADO=45°,
∴∠ADE=∠AED=45°,
∴AE=AD=2,
∴AE=AB=2AM,
∵AF∥OM,
∴$\frac{EF}{FO}$=$\frac{EA}{AM}$=2,
∴EF=2FO,EF=$\frac{2}{3}$EO,
∵OE=$\sqrt{E{M}^{2}+O{M}^{2}}$=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
∴EF=$\frac{2\sqrt{10}}{3}$,
故选D.
点评 本题主要考查切线的性质及正方形的性质、平行线分线段成比例定理等知识,掌握切线的性质是解题的关键,求得EF=2OF是解题的关键.

练习册系列答案
相关题目
7.cos30°的值是( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
14.太阳的表面温度大约有6000℃,而太阳中心的温度达到了1920万℃,其中“1920万”用科学记数法可将表示为( )
| A. | 1.92×103 | B. | 1.92×107 | C. | 19.2×102 | D. | 0.192×108 |
4. 如图,△P1OA1,△P2A1A2都是等腰直角三角形,点P1,P2都在函数y=$\frac{4}{x}$(x>0)的图象上,斜边OA1、A1A2都在x轴上,则点P2的坐标是( )
如图,△P1OA1,△P2A1A2都是等腰直角三角形,点P1,P2都在函数y=$\frac{4}{x}$(x>0)的图象上,斜边OA1、A1A2都在x轴上,则点P2的坐标是( )
 如图,△P1OA1,△P2A1A2都是等腰直角三角形,点P1,P2都在函数y=$\frac{4}{x}$(x>0)的图象上,斜边OA1、A1A2都在x轴上,则点P2的坐标是( )
如图,△P1OA1,△P2A1A2都是等腰直角三角形,点P1,P2都在函数y=$\frac{4}{x}$(x>0)的图象上,斜边OA1、A1A2都在x轴上,则点P2的坐标是( )| A. | (4$\sqrt{2}$,$\sqrt{2}$) | B. | (4+2$\sqrt{2}$,4-2$\sqrt{2}$) | C. | (2+2$\sqrt{2}$,2$\sqrt{2}$-2) | D. | (4+2$\sqrt{2}$,2+2$\sqrt{2}$) |
11.若正整数按如图所示的规律排列,则第8行第5列的数字是( )


| A. | 64 | B. | 56 | C. | 58 | D. | 60 |
8.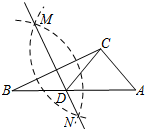 如图,在已知的△ABC中,按以下步骤作图:
如图,在已知的△ABC中,按以下步骤作图:
①分别以B、C为圆心,以大于$\frac{1}{2}$BC的长为半径作弧,两弧相交于两点M、N;②作直线MN交AB于点D,连接CD,若CD=AC,∠A=50°,则∠B=( )
 如图,在已知的△ABC中,按以下步骤作图:
如图,在已知的△ABC中,按以下步骤作图:①分别以B、C为圆心,以大于$\frac{1}{2}$BC的长为半径作弧,两弧相交于两点M、N;②作直线MN交AB于点D,连接CD,若CD=AC,∠A=50°,则∠B=( )
| A. | 50° | B. | 45° | C. | 30° | D. | 25° |
9.据河南省发改委发布消息,2016年全省固定资产投资继续保持持续稳定增长,全年完成39753亿元,总量居全国第3位.将数据39753亿用科学记数法表示为( )
| A. | 3.9753×109 | B. | 0.39753×1010 | C. | 39.753×1011 | D. | 3.9753×1012 |







