题目内容
13.现有以下命题:①平分弦的直径垂直平分弦,平分弦所对的弧;
②等弧所对的弦相等,所对的圆周角相等;
③边数相等的正多边形都相似;
④有一个角相等的两个等腰三角形相似.
正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据垂径定理,圆心角、弧、弦的关系,相似多边形的判定定理,相似三角形的判定进行判断即可.
解答 解:①应为“平分弦(不是直径)的直径垂直于弦,且平分弦所对的弧”,故错误;
②在同圆和等圆中,等弧所对的弦相等,所对的圆周角相等;故错误;
③边数相等的正多边形都相似;故正确;
④必须得是对应角相等才成立,即应强调这个角同是顶角还是底角或一个三角形的顶角等于另一个三角形的底角,故错误;
故选A.
点评 本题考查了命题与定理的知识,解题的关键是了解圆周角定理、垂径定理等知识,属于基础题,比较简单.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.(-1)2003+(-1)2004=( )
| A. | 0 | B. | -1 | C. | 1或者-1 | D. | 1 |
2.下列各数中,互为倒数的是( )
| A. | 0.1与1 | B. | 3与-$\frac{1}{3}$ | C. | -3与3 | D. | 2与$\frac{1}{2}$ |
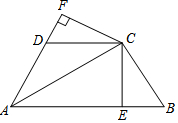 如图,已知AC平分∠BAD,CE⊥AB于点E,CF⊥AD于点F,且BC=CD.
如图,已知AC平分∠BAD,CE⊥AB于点E,CF⊥AD于点F,且BC=CD.