题目内容
3.计算:(1)($\sqrt{48}$-4$\sqrt{\frac{1}{8}}$)(3$\sqrt{\frac{1}{3}}$-2$\sqrt{0.5}$)
(2)($\sqrt{48}$+$\frac{1}{4}$$\sqrt{6}$)÷$\sqrt{27}$.
分析 (1)首先化简二次根式,然后利用多项式的乘法法则求解;
(2)首先化简二次根式,然后利用二次根式的除法法则求解.
解答 解:(1)原式=(4$\sqrt{3}$-$\sqrt{2}$)($\sqrt{3}$-$\sqrt{2}$)=12-$\sqrt{6}$-4$\sqrt{6}$+2=14-5$\sqrt{6}$;
(2)原式=(4$\sqrt{3}$+$\frac{\sqrt{6}}{4}$)÷3$\sqrt{3}$=$\frac{4}{3}$+$\frac{\sqrt{2}}{12}$.
点评 本题考查了二次根式的混合运算是二次根式乘法、除法及加减法运算法则的综合运用.学习二次根式的混合运算应注意:与有理数的混合运算一致,运算顺序先乘方再乘除,最后加减,有括号的先算括号里面的.

练习册系列答案
相关题目
13.现有以下命题:
①平分弦的直径垂直平分弦,平分弦所对的弧;
②等弧所对的弦相等,所对的圆周角相等;
③边数相等的正多边形都相似;
④有一个角相等的两个等腰三角形相似.
正确的有( )
①平分弦的直径垂直平分弦,平分弦所对的弧;
②等弧所对的弦相等,所对的圆周角相等;
③边数相等的正多边形都相似;
④有一个角相等的两个等腰三角形相似.
正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
13.如果把分式$\frac{x-y}{x+y}$中的x和y都扩大到原来的10倍,那么分式的值( )
| A. | 扩大到原来的10倍 | B. | 缩小到原来的 | ||
| C. | 是原来的 | D. | 不变 |
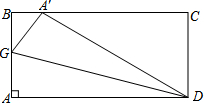 如图,ABCD是一张长方形纸片,且AD=2AB,沿过点D的折痕将∠A翻折,使得点A落在BC边上(即A′处),折痕交AB于点G,那么∠A′GD=75°.
如图,ABCD是一张长方形纸片,且AD=2AB,沿过点D的折痕将∠A翻折,使得点A落在BC边上(即A′处),折痕交AB于点G,那么∠A′GD=75°.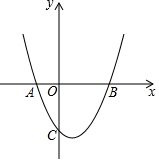 如图,抛物线y=x2-2x-3与x轴交于A、B两点,与y轴交于点C.
如图,抛物线y=x2-2x-3与x轴交于A、B两点,与y轴交于点C.