题目内容
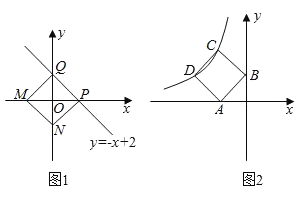
【题目】如图，抛物线y＝－x2＋bx＋c与x轴交于点A（－1，0），与y轴交于点B（0，2），直线y＝
x－1与y轴交于点C，与x轴交于点D，点P是线段CD上方的抛物线上一动点，过点P作PF垂直x轴于点F，交直线CD于点E，
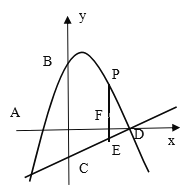
（1）求抛物线的解析式；
（2）设点P的横坐标为m，当线段PE的长取最大值时，解答以下问题．
①求此时m的值．
②设Q是平面直角坐标系内一点，是否存在以P、Q、C、D为顶点的平行四边形？若存在，直接写出点Q的坐标；若不存在，请说明理由．
【答案】（1）y＝﹣x2+x+2；（2）①m＝
；②存在以P、Q、C、D为顶点的四边形是平行四边形，点Q的坐标为
【解析】
（1）由题意利用待定系数法，即可求出抛物线的解析式；
（2）①由题意分别用含m的代数式表示出点P，E的纵坐标，再用含m的代数式表示出PE的长，运用函数的思想即可求出其最大值；
②根据题意对以P、Q、C、D为顶点的四边形是平行四边形分三种情况进行讨论与分析求解.
解：（1）将A（﹣1，0），B（0，2）代入y＝﹣x2+bx+c，得：
，解得：b=1,c=2
∴抛物线的解析式为y＝﹣x2+x+2．
（2）①∵直线y＝
x-1与y轴交于点C，与x轴交于点D，
∴点C的坐标为（0，-1），点D的坐标为（2，0），
∴0＜m＜2．
∵点P的横坐标为m，
∴点P的坐标为（m，﹣m2+m+2），点E的坐标为（m， m+3），
∴PE＝﹣m2+m+2﹣（ m+3）＝﹣m2+m+3＝﹣（m﹣）2+
．
∵﹣1＜0，0＜＜2，
∴当m＝时，PE最长．
②由①可知，点P的坐标为（，
）．
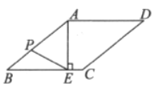
以P、Q、C、D为顶点的四边形是平行四边形分三种情况（如图所示）：
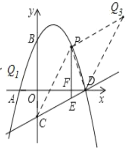
①以PD为对角线，点Q的坐标为
；
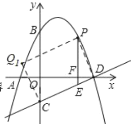
②以PC为对角线，点Q的坐标为
；
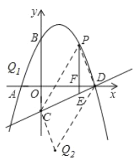
③以CD为对角线，点Q的坐标为
．
综上所述：在（2）的情况下，存在以P、Q、C、D为顶点的四边形是平行四边形，点Q的坐标为.
