题目内容
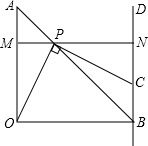 如图,△AOB是等腰直角三角形,直线BD∥OA,OB=OA=1,P是线段AB上一动点,过P点作MN∥OB,分别交OA、BD于M、N,PC⊥PO,交BD于点C.
如图,△AOB是等腰直角三角形,直线BD∥OA,OB=OA=1,P是线段AB上一动点,过P点作MN∥OB,分别交OA、BD于M、N,PC⊥PO,交BD于点C.(1)求证:OP=PC;
(2)当点C在射线BN上时,设AP长为m,四边形POBC的面积为S,请求出S与m间的函数关系式,并写出自变量m的取值范围;
(3)当点P在线段AB上移动时,点C也随之在直线BN上移动,△PBC是否可能成为等腰三角形?如果可能,求出所有能使△PBC成为等腰三角形时的PM的值;如果不可能,请说明理由.
考点:四边形综合题
专题:几何综合题,分类讨论
分析:(1)首先利用矩形的判定得出四边形OBNM为矩形,即可得出∠CPN=∠POM,进而得出△OPM≌△PCN,求出即可;
(2)利用S=S△OPB+S△PBC进而得出S与m的函数关系;
(3)利用①当点P与点A重合时,PC=BC=1,②如图②,当点C在OB下方,且PB=CB时,分别求出即可.
(2)利用S=S△OPB+S△PBC进而得出S与m的函数关系;
(3)利用①当点P与点A重合时,PC=BC=1,②如图②,当点C在OB下方,且PB=CB时,分别求出即可.
解答:(1)证明:如图①,△AOB是等腰直角三角形,AO=BO=1,
∴∠A=45°,∠AOB=90°,
直线BN∥OA,MN∥OB,
∴四边形OBNM为矩形,
∴MN=OB=1,∠PMO=∠CNP=90°
而∠AMP=90°,∠A=∠APM=∠BPN=45°,
∴OM=BN=PN,
∵∠OPC=90°,
∴∠OPM+∠CPN=90°,
又∵∠OPM+∠POM=90°,
∴∠CPN=∠POM,
在△OPM和△PCN中
,
∴△OPM≌△PCN(ASA),
∴OP=PC,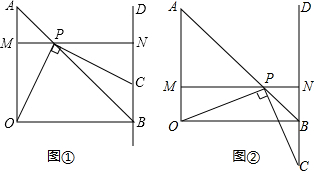
(2)解:∵AM=PM=APsin45°=
m,
∴NC=PM=
m,∴BN=OM=PN=1-
m;
∴BC=BN-NC=1-
m-
m=1-
m,
S=S△OPB+S△PBC=
BO•MO+
BC•PN,
=
m2-
m+1(0≤m≤
);
(3)解:△PBC可能为等腰三角形,
①当点P与点A重合时,PC=BC=1,此时PM=0,
②如图②,当点C在OB下方,且PB=CB时,
有OM=BN=PN=1-
m,
∴BC=PB=
PN=
-m,
∴NC=BN+BC=1-
m+
-m,
由(2)知:NC=PM=
m,
∴1-
m+
-m=
m,
∴m=1.
∴PM=
m=
;
∴使△PBC为等腰三角形时的PM的值为0或
.
∴∠A=45°,∠AOB=90°,
直线BN∥OA,MN∥OB,
∴四边形OBNM为矩形,
∴MN=OB=1,∠PMO=∠CNP=90°
而∠AMP=90°,∠A=∠APM=∠BPN=45°,
∴OM=BN=PN,
∵∠OPC=90°,
∴∠OPM+∠CPN=90°,
又∵∠OPM+∠POM=90°,
∴∠CPN=∠POM,
在△OPM和△PCN中
|
∴△OPM≌△PCN(ASA),
∴OP=PC,

(2)解:∵AM=PM=APsin45°=
| ||
| 2 |
∴NC=PM=
| ||
| 2 |
| ||
| 2 |
∴BC=BN-NC=1-
| ||
| 2 |
| ||
| 2 |
| 2 |
S=S△OPB+S△PBC=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 2 |
| ||
| 2 |
(3)解:△PBC可能为等腰三角形,
①当点P与点A重合时,PC=BC=1,此时PM=0,
②如图②,当点C在OB下方,且PB=CB时,
有OM=BN=PN=1-
| ||
| 2 |
∴BC=PB=
| 2 |
| 2 |
∴NC=BN+BC=1-
| ||
| 2 |
| 2 |
由(2)知:NC=PM=
| ||
| 2 |
∴1-
| ||
| 2 |
| 2 |
| ||
| 2 |
∴m=1.
∴PM=
| ||
| 2 |
| ||
| 2 |
∴使△PBC为等腰三角形时的PM的值为0或
| ||
| 2 |
点评:此题主要考查了四边形综合以及矩形的性质和判定以及等腰三角形的性质、全等三角形的判定与性质等知识,利用分类讨论得出是解题关键.

练习册系列答案
相关题目
 如图,在梯形ABCD中,AB∥CD,E是BC的中点,AB+CD=AD,求证:
如图,在梯形ABCD中,AB∥CD,E是BC的中点,AB+CD=AD,求证: 如图,一艘货轮由港口A出发向正东方向行驶,在港口A处时,测得灯塔B在港口A的南偏东30°方向,小岛C在港口A的南偏东60°方向,当这艘货轮行驶60海里到点D处时,小岛C恰好在点D处的正南方向,此时测得灯塔B在南偏西60°的方向,求:
如图,一艘货轮由港口A出发向正东方向行驶,在港口A处时,测得灯塔B在港口A的南偏东30°方向,小岛C在港口A的南偏东60°方向,当这艘货轮行驶60海里到点D处时,小岛C恰好在点D处的正南方向,此时测得灯塔B在南偏西60°的方向,求: 如图,在△ABC中,AB=AC,AD是BC边上的中线,四边形ADBE是平行四边形,求证:四边形ADBE是矩形.
如图,在△ABC中,AB=AC,AD是BC边上的中线,四边形ADBE是平行四边形,求证:四边形ADBE是矩形. 已知:如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数
已知:如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数