题目内容
7.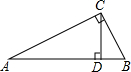 如图,在Rt△ABC中,∠ACB=90°,CD为斜边AB上的高,点D为垂足,BC=8,BD=5,求sinA,sin∠ACD.
如图,在Rt△ABC中,∠ACB=90°,CD为斜边AB上的高,点D为垂足,BC=8,BD=5,求sinA,sin∠ACD.
分析 根据在Rt△ABC中,∠ACB=90°,CD为斜边AB上的高,点D为垂足,BC=8,BD=5,可得CD的长,∠A=∠BCD,∠ACD=∠B,从而可以求得sinA,sin∠ACD的值.
解答 解:∵在Rt△ABC中,∠ACB=90°,CD为斜边AB上的高,
∴CD=$\sqrt{B{C}^{2}-B{D}^{2}}=\sqrt{{8}^{2}-{5}^{2}}=\sqrt{39}$.
∴sinB=$\frac{CD}{BC}=\frac{\sqrt{39}}{8}$,sin∠BCD=$\frac{BD}{BC}=\frac{5}{8}$.
∵∠ACB=90°,CD为斜边AB上的高,
∴∠BDC=90°.
∴∠B+∠BCD=90°,∠B+∠A=90°,∠ACD+∠BCD=90°.
∴∠A=∠BCD,∠ACD=∠B.
∴sinA=sin∠BCD=$\frac{BD}{BC}=\frac{5}{8}$,sin∠ACD=sinB=$\frac{CD}{BC}=\frac{\sqrt{39}}{8}$.
即sinA=$\frac{5}{8}$,sin∠ACD=$\frac{\sqrt{39}}{8}$.
点评 本题考查解直角三角形,解题的关键是利用数学中转化的思想,进行角的转化,从而可以求得所求角的函数值.

练习册系列答案
相关题目
19.甲、乙两名同学本学期参加的11次考试成绩(单位:分)如下表所示:
(1)求两人的平均分及方差;
(2)分析他们的成绩各有什么特点;
(3)现要从两人中选一人参加比赛,历届比赛成绩表明,平均成绩达98分以上(含98分)才可能迸人决赛,你认为应该选谁参加这次比赛呢?为什么?
| 甲 | 98 | 100 | 100 | 90 | 96 | 91 | 89 | 99 | 100 | 100 | 93 |
| 乙 | 98 | 99 | 96 | 94 | 95 | 92 | 92 | 98 | 96 | 99 | 97 |
(2)分析他们的成绩各有什么特点;
(3)现要从两人中选一人参加比赛,历届比赛成绩表明,平均成绩达98分以上(含98分)才可能迸人决赛,你认为应该选谁参加这次比赛呢?为什么?
17.以下说法正确的是( )
| A. | 每个内角都是120°的六边形一定是正六边形 | |
| B. | 正n边形的对称轴不一定有n条 | |
| C. | 正n边形的每一个外角度数等于它的中心角度数 | |
| D. | 正多边形一定既是轴对称图形,又是中心对称图形 |