题目内容
13.用配方法把下列函数化成y=a(x-h)2的形式,并写出函数图象的顶点坐标、开口方向及对称轴.(1)y=4x2-4x+1;
(2)y=$\frac{1}{2}$x2+2x+2;
(3)y=-$\frac{1}{3}$x2+$\frac{2}{3}$$\sqrt{3}$x-1.
分析 (1)直接利用配方法得出二次函数顶点坐标和对称轴即可;
(2)直接利用配方法得出二次函数顶点坐标和对称轴即可;
(3)直接利用配方法得出二次函数顶点坐标和对称轴即可.
解答 解:(1)y=4x2-4x+1
=4(x2-x+$\frac{1}{4}$)
=4(x-$\frac{1}{2}$)2,
函数图象的顶点坐标为:($\frac{1}{2}$,0)、开口方向向上,对称轴为:x=$\frac{1}{2}$;
(2)y=$\frac{1}{2}$x2+2x+2
=$\frac{1}{2}$(x2+4x+4)
=$\frac{1}{2}$(x+2)2,
函数图象的顶点坐标为:(-2,0)、开口方向向上,对称轴为:x=-2;
(3)y=-$\frac{1}{3}$x2+$\frac{2}{3}$$\sqrt{3}$x-1
=-$\frac{1}{3}$(x2-2$\sqrt{3}$x+3)
=-$\frac{1}{3}$(x-$\sqrt{3}$)2,
函数图象的顶点坐标为:($\sqrt{3}$,0)、开口方向向下,对称轴为:x=$\sqrt{3}$.
点评 此题主要考查了配方法求二次函数顶点坐标和对称轴,正确应用配方法求出是解题关键.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
1.在下列四个一元二次方程中,没有实数根的一个是( )
| A. | x2-8x+1=0 | B. | 2x2+1=3x | C. | 3x2-6x+4=0 | D. | (x-2)2-1=0 |
 如图,AC与BD相交于O点,已知AO=DO,∠A=∠D,求证:AB=DC.
如图,AC与BD相交于O点,已知AO=DO,∠A=∠D,求证:AB=DC. 拦水坝横断面如图所示,迎水坡AB的坡比是1:$\sqrt{3}$,坝高BC=10m,则坡面AB的长度是20m.
拦水坝横断面如图所示,迎水坡AB的坡比是1:$\sqrt{3}$,坝高BC=10m,则坡面AB的长度是20m.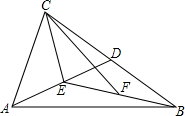 如图,△ABC中,D、E、F分别为BC、AD、DE的中点,若S△CEF=2.求S△ABC.
如图,△ABC中,D、E、F分别为BC、AD、DE的中点,若S△CEF=2.求S△ABC.