题目内容
 如图,已知MN⊥PQ,垂足为O,点A、A1是以MN为对称轴的对称点,而点A、A2是以PQ为对称点,则点A1A2关于点O成中心对称,你能说明其中的道理吗?
如图,已知MN⊥PQ,垂足为O,点A、A1是以MN为对称轴的对称点,而点A、A2是以PQ为对称点,则点A1A2关于点O成中心对称,你能说明其中的道理吗?考点:中心对称,轴对称的性质
专题:
分析:根据轴对称的对称点被对称轴垂直平分,可得MN是AA1的垂直平分线,PQ是AA2的垂直平分线,根据垂直平分线的性质,可得OA=OA1,∠3=∠4,OA=OA2,∠1=∠2,再根据中心对称的性质,可得答案.
解答:证明:如图:
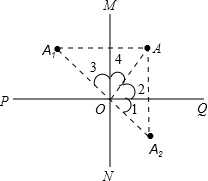
连结AA1,AA2,OA,OA1,OA2,
∵A,A1是以MN为对称轴的对称点,
∴OA=OA1,∠3=∠4,
同理OA=OA2,∠1=∠2.
∴OA1=OA2,且∠1+∠2+∠3+∠4=2(∠2+∠4)=2×90°=180°,
∴A1,A2是以O为对称中心的对称点.

连结AA1,AA2,OA,OA1,OA2,
∵A,A1是以MN为对称轴的对称点,
∴OA=OA1,∠3=∠4,
同理OA=OA2,∠1=∠2.
∴OA1=OA2,且∠1+∠2+∠3+∠4=2(∠2+∠4)=2×90°=180°,
∴A1,A2是以O为对称中心的对称点.
点评:本题考查了中心对称,利用了轴对称的性质,中心对称的性质.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
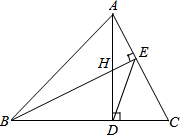 如图所示,△ABC的高AD、BE相交于点H,若BH=AC,则下列结论:
如图所示,△ABC的高AD、BE相交于点H,若BH=AC,则下列结论:①AE=CE;②∠ABC=45°;③DH=DC;④∠CED=45°
成立的有( )
| A、①② | B、①②③ |
| C、②③④ | D、①②③④ |
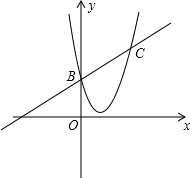 如图,在平面直角坐标系中,一次函数y=
如图,在平面直角坐标系中,一次函数y=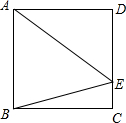 如图,在正方形ABCD中,点E在CD边上,且CE:DE=1:3,求∠AEB的正弦值.
如图,在正方形ABCD中,点E在CD边上,且CE:DE=1:3,求∠AEB的正弦值.