题目内容
在平面直角坐标系中,抛物线y=x2+5x+4的顶点为M,与x轴交于A,B两点,与y轴交于C点.
(1)求点A,B,C的坐标;
(2)求抛物线y=x2+5x+4关于坐标原点O对称的抛物线的函数表达式;
(3)设(2)中所求抛物线的顶点为M′,与x轴交于A′,B′两点,与y轴交于C′点,在以A,B,C,M,A′,B′,C′,M′这八个点中的四个点为顶点的平行四边形中,求其中一个不是菱形的平行四边形的面积.
解:(1)令y=0,得x2+5x+4=0,
∴x1=﹣4,x2=﹣1,
令x=0,得y=4,
∴A(﹣4,0),B(﹣1,0),C(0,4).
(2)∵A,B,C关于坐标原点O对称后的点为(4,0),(1,0),(0,﹣4),
∴所求抛物线的函数表达式为y=ax2+bx﹣4,
将(4,0),(1,0)代入上式,得
解得: ,
,
∴y=﹣x2+5x﹣4.
(3)如图,取四点A,M,A′,M′,连接AM,MA′,A′M′,M′A,MM′,
由中心对称性可知,MM′过点O,OA=OA′,OM=OM′,
∴四边形AMA′M′为平行四边形,
又知AA′与MM′不垂直,
∴平行四边形AMA′M′不是菱形,
过点M作MD⊥x轴于点D,

∵y= ,
,
∴M( ),
),
又∵A(﹣4,0),A′(4,0)
∴AA′=8,MD= ,
,
∴ =
=

 科学实验活动册系列答案
科学实验活动册系列答案色盲是伴X染色体隐性先天遗传病,患者中男性远多于女性,从男性体检信息库中随
机抽取体检表,统计结果如下表:
| 抽取的体检表数n | 50 | 100 | 200 | 400 | 500 | 800 | 1000 | 1200] | 1500 | 2000 |
| 色盲患者的频数m | 3 | 7 | 13 | 29 | 37 | 55 | 69 | 85 | 105 | 138 |
| 色盲患者的频率m/n | 0.060 | 0.070 | 0.065 | 0.073 | 0.074 | 0.069 | 0.069 | 0.071 | 0.070 | 0.069 |
根据上表,估计在男性中,男性患色盲的概率为 (结果精确到0.01)
 恰有两个整数解,则m的取值范围是( )
恰有两个整数解,则m的取值范围是( )



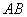 于点
于点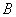 ,点
,点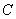 在
在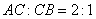 ,点
,点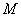 是直线上的动点,作点
是直线上的动点,作点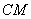 的对称点
的对称点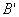 ,直线
,直线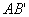 与直线
与直线 ,连接
,连接
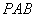 = °,线段
= °,线段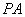 与
与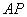 相交于
相交于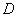 ,
, 。
。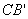 ;②
;②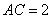 ,
, ,则满足条件
,则满足条件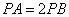 的点都在一个确定的圆上,在
的点都在一个确定的圆上,在
 )﹣1+|
)﹣1+| ﹣1|﹣3tan30°+6
﹣1|﹣3tan30°+6 .
.