题目内容
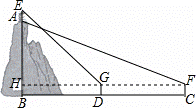
如图,直线⊥线段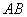 于点
于点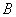 ,点
,点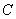 在
在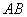 上,且
上,且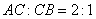 ,点
,点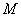 是直线上的动点,作点
是直线上的动点,作点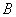 关于直线
关于直线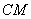 的对称点
的对称点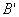 ,直线
,直线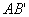 与直线
与直线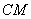 相交于点
相交于点 ,连接
,连接
(1)如图1,若点 与点
与点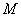 重合,则∠
重合,则∠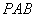 = °,线段
= °,线段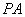 与
与 的比值为 ;
的比值为 ;
(2)如图2,若点 与点
与点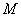 不重合,设过
不重合,设过 、
、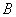 、
、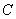 三点的圆与直线
三点的圆与直线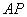 相交于
相交于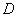 ,
,
连接 。
。
求证:① =
=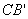 ;②
;②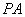 =2
=2 ;
;
(3)如图3,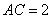 ,
, ,则满足条件
,则满足条件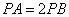 的点都在一个确定的圆上,在
的点都在一个确定的圆上,在
以下两小题中选做一题:
①如果你能发现这个确定圆的圆心和半径,那么不必写出发现过程,只要证明这个
圆上的任意一点Q,都满足QA=2QB
②如果你不能发现这个确定圆的圆心和半径,那么请取几个特殊位置的 点,如点
点,如点 在直线
在直线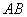 上、点
上、点 与点
与点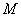 重合等进行探究,求这个圆的半径
重合等进行探究,求这个圆的半径




(3)定圆如图所示



练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
我们解一元二次方程3x2﹣6x=0时,可以运用因式分解法,将此方程化为3x(x﹣2)=0,从而得到两个一元一次方程:3x=0或x﹣2=0,进而得到原方程的解为x1=0,x2=2.这种解法体现的数学思想是( )
|
| A. | 转化思想 | B. | 函数思想 | C. | 数形结合思想 | D. | 公理化思想 |
一元一次不等式组 的解集中,整数解的个数是( )
的解集中,整数解的个数是( )
|
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |




 ﹣1
﹣1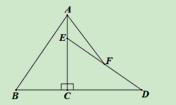

 处,折痕交CD边于点E,连接BE
处,折痕交CD边于点E,连接BE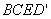 是平行四边形
是平行四边形

 取1.732,结果保留整数)
取1.732,结果保留整数)