题目内容
17.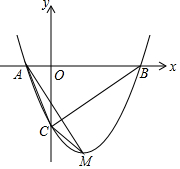 如图,在平面直角坐标系中,抛物线y=x2-2x-3与x轴交于点A,B,与y轴交于点C
如图,在平面直角坐标系中,抛物线y=x2-2x-3与x轴交于点A,B,与y轴交于点C(1)求△ABC的面积;
(2)点C关于此抛物线的对称轴的对称点是D,若过点D的直线与此抛物线只有一个交点,求此直线的表达式;
(3)小敏发现有过A,B两点的抛物线如果与y负半轴交于点C′,M为抛物线的顶点,那么△AC′M与△AC′B的面积比不变,请你求出这个比值.
分析 (1)分别求出A、B、C三点坐标,根据三角形的面积公式计算即可.
(2)设过点D的直线为y=kx+b,把D(2,-3)代入,得-3=2k+b,得b=-3-2k,得y=kx-3-2k,由$\left\{\begin{array}{l}{y=kx-3-2k}\\{y={x}^{2}-2x-3}\end{array}\right.$,消去y得x2-(2+k)x+2k=0,根据△=0,列出方程即可解决问题.
(3)设过A、B两点的抛物线的解析式为y=a(x+1)(x-3)=ax2-2ax-3a,求出C′、M′坐标,再求出△AC′M与△AC′B的面积(用a表示),即可解决问题.
解答 解:(1)对于抛物线y=x2-2x-3,
令x=0得y=-3,
∴C(0,-3),
令y=0得x2-2x-3=0,解得x=3或-1,
∴A(-1,0),B(3,0),
∴AB=4,CO=3,
∴S△ABC=$\frac{1}{2}$•AB•OC═$\frac{1}{2}$×3×4=6.
(2)如图1中,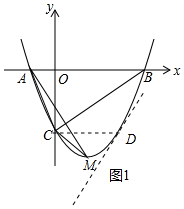
∵抛物线的对称轴x=1,点C坐标(0,-3),C、D关于对称轴对称,
∴D(2,-3),设过点D的直线为y=kx+b,把D(2,-3)代入,
得-3=2k+b,
∴b=-3-2k,
∴y=kx-3-2k,
由$\left\{\begin{array}{l}{y=kx-3-2k}\\{y={x}^{2}-2x-3}\end{array}\right.$,消去y得x2-(2+k)x+2k=0,
由题意,△=0,
∴(2+k)2-8k=0,
∴k=2,
∴直线CD的解析式为y=2x-7.
(3)如图2中,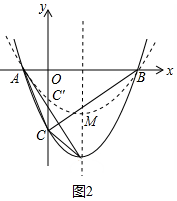
设过A、B两点的抛物线的解析式为y=a(x+1)(x-3)=ax2-2ax-3a,
∴C′(0,-3a),M(1,-4a),
∴S△AC′M=S△AOC′+S△OC′M-S△AOM=$\frac{1}{2}$•1•3a+$\frac{1}{2}$•3a•1-$\frac{1}{2}$•1•4a=a,
S△ABC′=$\frac{1}{2}$•4•3a=6a,
∴S△AC′M:S△AC′B=a:6a=1:6.
点评 本题考查二次函数与坐标轴的交点、直线与抛物线的位置关系、三角形的面积问题等知识,解题的关键是学会用转化的思想思考问题,学会用分割法求三角形面积,属于中考常考题型.

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案| A. | 平行四边形 | B. | 菱形 | C. | 矩形 | D. | 任意四边形 |
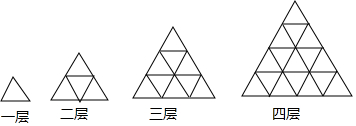
| 层数 | 1 | 2 | 3 | 4 | … | n |
| 所含小三角形的个数 | 1 | 4 | 9 | 16 | … | 4n-3 |
| 所需小木棒的根数 | 3 | 9 | 18 | 30 | … | $\frac{3}{2}$n(n+1) |
| A. | 若a-c=b-c,则a=b | B. | 若a=2,则a2=2a | C. | 若ax=bx,则a=x | D. | 若$\frac{a}{x}$=$\frac{b}{x}$,则a=b |
| A. | $\sqrt{6}$+$\sqrt{3}$=3 | B. | 3$\sqrt{2}$-$\sqrt{2}$=3 | C. | $\sqrt{2}$×$\sqrt{8}$=4 | D. | $\sqrt{6}$÷$\sqrt{3}$=2 |
| A. | 5℃ | B. | 13℃ | C. | 8℃ | D. | 3℃ |
 如图,点D是△ABC的边AC的上一点,且∠ABD=∠C;如果$\frac{AD}{CD}$=$\frac{1}{3}$,那么$\frac{BD}{BC}$=( )
如图,点D是△ABC的边AC的上一点,且∠ABD=∠C;如果$\frac{AD}{CD}$=$\frac{1}{3}$,那么$\frac{BD}{BC}$=( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |