题目内容
1.已知a,b,c分别△ABC的三边,且满足a2c2-b2c2=a4-b4,试判断△ABC的形状为直角三角形或等腰三角形或等腰直角三角形.分析 将等式右边的移项到方程左边,然后提取公因式将方程左边分解因式,根据两数相乘积为0,两因式中至少有一个数为0转化为两个等式;根据等腰三角形的判定,以及勾股定理的逆定理得出三角形为直角三角形或等腰三角形.
解答 解:∵a2c2-b2c2=a4-b4,
∴c2(a2-b2)=(a2+b2)(a2-b2),
移项得:c2(a2-b2)-(a2+b2)(a2-b2)=0,
因式分解得:(a2-b2)[c2-(a2+b2)]=0,
则当a2-b2=0时,a=b;当a2-b2≠0时,a2+b2=c2;
所以△ABC是直角三角形或等腰三角形或等腰直角三角形.
故答案是:直角三角形或等腰三角形或等腰直角三角形.
点评 此题考查因式分解和勾股定理逆定理的实际运用,掌握平方差公式和完全平方公式是关键.

练习册系列答案
相关题目
9.使$\sqrt{a-1}$有意义的a的取值范围是( )
| A. | a>1 | B. | a≤1 | C. | a<1 | D. | a≥1 |
6.已知线段a=l,c=5,线段b是线段a、c的比例中项,线段b的值为( )
| A. | 2.5 | B. | $\sqrt{5}$ | C. | ±2.5 | D. | ±$\sqrt{5}$ |
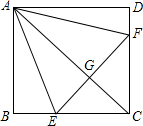 如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,求证:
如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,求证: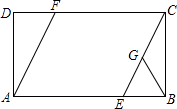 已知:如图,在矩形ABCD中,点E,F分别在AB,CD边上,连接CE,AF.若CE=AF
已知:如图,在矩形ABCD中,点E,F分别在AB,CD边上,连接CE,AF.若CE=AF