题目内容
△ABC中,BD平分∠ABC,CE平分∠ACB,BD与CE交于点M.
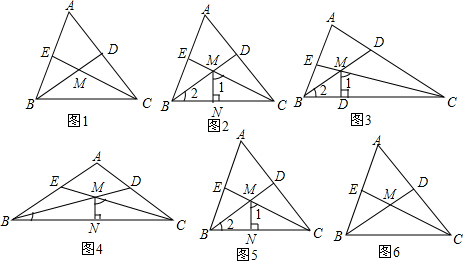
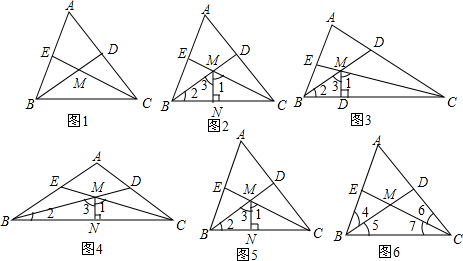
(1)如图1,若∠BAC=60°,则∠BMC= .
(2)如图2,若MN⊥BC于N,∠BAC=60°,则图中∠1-∠2= .
(3)如图3,若MN⊥BC于N,∠BAC=90°,则图中∠1-∠2= .
(4)如图4,若MN⊥BC于N,∠BAC=120°,则图中∠1-∠2= .
(5)如图5,若MN⊥BC于N,∠BAC=α,求出图中∠1-∠2的度数.
(6)如图6,若∠BEC=α,∠BDC=β,那么∠BMC= (用含α、β的代数式表示).
(1)如图1,若∠BAC=60°,则∠BMC=
(2)如图2,若MN⊥BC于N,∠BAC=60°,则图中∠1-∠2=
(3)如图3,若MN⊥BC于N,∠BAC=90°,则图中∠1-∠2=
(4)如图4,若MN⊥BC于N,∠BAC=120°,则图中∠1-∠2=
(5)如图5,若MN⊥BC于N,∠BAC=α,求出图中∠1-∠2的度数.
(6)如图6,若∠BEC=α,∠BDC=β,那么∠BMC=

考点:三角形内角和定理,三角形的外角性质
专题:
分析:(1)在△ABC中,根据角平分线的定义及三角形内角和定理,先求得∠ABD+∠ACE的值,从而求得∠CBD+∠ECB的值;然后在△BMC中利用三角形内角和定理求得∠BMC度数;
(2)同(1)可得∠BMC=120°,进而可得∠1+∠3=120°①,由MN⊥BC可得:∠2+∠3=90°②,然后①-②即可得到∠1-∠2 的度数;
(3)同(1)可得∠BMC=135°,然后同(2)得∠1+∠3=135°①,由MN⊥BC可得:∠2+∠3=90°②,然后①-②即可得到∠1-∠2 的度数;
(4)同(3)可得∠1-∠2 的度数;
(5)同上先用∠α表示∠BMC的度数=90°+
∠α,然后表示∠1+∠3=90°+
∠α,然后由∠2+∠3=90°,两式相减即可得到∠1-∠2 的度数;
(6)利用外角的性质及上面(5)的结论即可用含α、β的代数式表示∠BMC=60°+
.
(2)同(1)可得∠BMC=120°,进而可得∠1+∠3=120°①,由MN⊥BC可得:∠2+∠3=90°②,然后①-②即可得到∠1-∠2 的度数;
(3)同(1)可得∠BMC=135°,然后同(2)得∠1+∠3=135°①,由MN⊥BC可得:∠2+∠3=90°②,然后①-②即可得到∠1-∠2 的度数;
(4)同(3)可得∠1-∠2 的度数;
(5)同上先用∠α表示∠BMC的度数=90°+
| 1 |
| 2 |
| 1 |
| 2 |
(6)利用外角的性质及上面(5)的结论即可用含α、β的代数式表示∠BMC=60°+
| α+β |
| 3 |
解答:解:(1)如图1,
∵BD、CE分别平分∠ABC和∠ACB,
∴∠ABD=∠CBD,∠ACE=∠ECB;
∵∠A+∠ABC+∠ACB=180°,
∴∠A+2∠CBD+2∠ECB=180°;
∵∠A=60°,
∴∠CBD+∠ECB=60°;
在△BMC中,
又∵∠BMC+∠CBD+∠ECB=180°,
∴∠BMC=120°.
故答案为:120°;
(2)同(1)可得∠BMC=120°,
∴∠1+∠3=120°①,
∵MN⊥BC,
∴∠2+∠3=90°②,
①-②得:∠1-∠2=30°,
故答案为:30°;
(3)同(1)可得∠BMC=135°,同(2)得∠1+∠3=135°①,
∵MN⊥BC,
∴∠2+∠3=90°②,
∴①-②得:∠1-∠2=45°,
故答案为:45°;
(4)同(3)可得∠1-∠2=60°,
故答案为:60°;
(5)同上可得:∠BMC=90°+
∠α,
∴∠1+∠3=90°+
∠α①,
∵∠2+∠3=90°②,
①-②得:
∠1-∠2=
∠α;
(6)由(5)可得∠BMC=90°+
∠A,
∵∠BEC=∠A+∠6,∠BDC=∠A+∠4,且∠4=∠5,∠6=∠7,
∴α=∠A+∠7①,β=∠A+∠5②,
①+②得:α+β=2∠A+(∠7+∠5),
∵∠BMC=90°+
∠A,
∴∠A=2∠BMC-180°,
∵∠7+∠5=180°-∠BMC,
∴α+β=4∠BMC-360°+180-∠BMC,
∴∠BMC=60°+
.
故答案为:60°+
.

∵BD、CE分别平分∠ABC和∠ACB,
∴∠ABD=∠CBD,∠ACE=∠ECB;
∵∠A+∠ABC+∠ACB=180°,
∴∠A+2∠CBD+2∠ECB=180°;
∵∠A=60°,
∴∠CBD+∠ECB=60°;
在△BMC中,
又∵∠BMC+∠CBD+∠ECB=180°,
∴∠BMC=120°.
故答案为:120°;
(2)同(1)可得∠BMC=120°,
∴∠1+∠3=120°①,
∵MN⊥BC,
∴∠2+∠3=90°②,
①-②得:∠1-∠2=30°,
故答案为:30°;
(3)同(1)可得∠BMC=135°,同(2)得∠1+∠3=135°①,
∵MN⊥BC,
∴∠2+∠3=90°②,
∴①-②得:∠1-∠2=45°,
故答案为:45°;
(4)同(3)可得∠1-∠2=60°,
故答案为:60°;
(5)同上可得:∠BMC=90°+
| 1 |
| 2 |
∴∠1+∠3=90°+
| 1 |
| 2 |
∵∠2+∠3=90°②,
①-②得:
∠1-∠2=
| 1 |
| 2 |
(6)由(5)可得∠BMC=90°+
| 1 |
| 2 |
∵∠BEC=∠A+∠6,∠BDC=∠A+∠4,且∠4=∠5,∠6=∠7,
∴α=∠A+∠7①,β=∠A+∠5②,
①+②得:α+β=2∠A+(∠7+∠5),
∵∠BMC=90°+
| 1 |
| 2 |
∴∠A=2∠BMC-180°,
∵∠7+∠5=180°-∠BMC,
∴α+β=4∠BMC-360°+180-∠BMC,
∴∠BMC=60°+
| α+β |
| 3 |
故答案为:60°+
| α+β |
| 3 |
点评:此题考查了三角形内角和定理、角平分线的性质及外角的性质,几个问题的设计具有层次性,一问扣一问,层层深入,解题的关键是:由浅入深,探寻规律.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知△ACD与△BCE,AD与BE相交于P点,若AC=BC,AD=BE,∠ACE=55°,∠BCD=155°,则∠BPD的度数为( )
如图,已知△ACD与△BCE,AD与BE相交于P点,若AC=BC,AD=BE,∠ACE=55°,∠BCD=155°,则∠BPD的度数为( )| A、110° | B、125° |
| C、130° | D、155° |
绝对值大于-3,且小于6的所有整数的个数是( )
| A、6个 | B、7个 |
| C、10个 | D、11个 |
下列图案中,是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
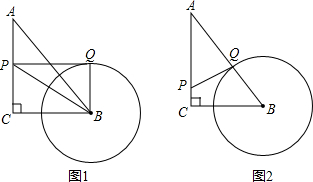
 如图,∠C=90°,以AC为半径的圆C与AB相交于点D.若AC=3,CB=4,求BD长.
如图,∠C=90°,以AC为半径的圆C与AB相交于点D.若AC=3,CB=4,求BD长.