��Ŀ����
5�� ��ֱ�DZ߳�Ϊ6�ĵ���ֱ�ǡ�AOC����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬��C��A�ֱ���x�ᣬy����������ϣ�һ�������߾�����A��C����B��-3��0����
��ֱ�DZ߳�Ϊ6�ĵ���ֱ�ǡ�AOC����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬��C��A�ֱ���x�ᣬy����������ϣ�һ�������߾�����A��C����B��-3��0������1����������ߵĽ���ʽ��
��2������P���߶�BC��һ���㣬����P��AB��ƽ���߽�AC�ڵ�E������AP������APE��������ʱ�����P�����ꣻ
��3������P��t��t�����������ϣ���Ƶ�PΪ�����ߵIJ����㣬����1���е������߽���ƽ�ƣ�ƽ�ƺ�������ֻ��һ�������㣬�Ҷ�����ֱ��y=2x-$\frac{7}{4}$�ϣ����ʱ�����ߵĽ���ʽ��
���� ��1����֪��������x��������������꣬�����������߷���Ϊ����ʽ��y=a��x+3����x-6����Ȼ��ѵ�A���������ú�������ʽ�������ϵ��a��ֵ��
��2���������������ε����ʵó�S��PCE=$\frac{��m-6��^{2}}{3}$�����������APE�����S�����ɵó���P���ꣻ
��3�������������ϲ�����Ķ����Լ�������ĸ����ó�����h-k=$\frac{3}{4}$�٣�����ƽ�ƺ�������ߵĶ�����ֱ��y=2x-$\frac{7}{4}$�ϣ��ó�����k=2k-$\frac{7}{4}$�ڣ������ⷽ���鼴�ɣ�
��� �⣺��1����B��-3��0����C��6��0������������Ϊy=a��x+3����x-6������A��0��6��
��6=a��0+3����0-6����
���a=-$\frac{1}{3}$��
��y=-$\frac{1}{3}$��x+3����x-6����
��y=-$\frac{1}{3}$x2+x+6��
��2����P��m��0����
��ͼ��
��PE��AB��
���PCE�ס�BCA��
��$\frac{{S}_{��PCE}}{{S}_{��BCA}}=\frac{P{C}^{2}}{B{C}^{2}}$��
$\frac{{S}_{��PCE}}{27}=\frac{��m-6��^{2}}{81}$��
��S��PCE=$\frac{��m-6��^{2}}{3}$��
��S=S��APC-S��PCE=-$\frac{1}{3}$m2+m+6��
=-$\frac{1}{3}$��m-$\frac{3}{2}$��2+$\frac{27}{4}$��
�൱m=$\frac{3}{2}$ʱ��S�����ֵΪ$\frac{27}{4}$��
��P��$\frac{3}{2}$��0����
��3����ƽ�ƺ�������ߵĶ���ΪG��h��k����
�������߽���ʽΪy=-$\frac{1}{3}$��x-h��2+k��
�������ߵIJ�����Ķ��壬�ã�t=-$\frac{1}{3}$��t-h��2+k��
����t2+��3-2h��t+h2-3k=0��
��ƽ�ƺ�������ֻ��һ�������㣬
��˷�����������ȵ�ʵ������
���=��3-2h��2-4��h2-3k��=0��
��h-k=$\frac{3}{4}$�٣�
�߶�����ֱ��y=2x-$\frac{7}{4}$�ϣ�
��k=2k-$\frac{7}{4}$�ڣ�
�������٢ڵã�h=1��k=$\frac{1}{4}$��
�������ߵĽ���ʽΪy=-$\frac{1}{3}$��x-1��2+$\frac{1}{4}$=-$\frac{1}{3}$x2+$\frac{2}{3}$x-$\frac{1}{12}$��
���� ������κ����ۺ��⣬��Ҫ�����˴���ϵ���������������ε����ʺ��ж��������ļ�ֵ���¶��弰һԪ���η��̸���������Ȿ��Ĺؼ��������¶��壬��һ���е��Ѷȵ���Ŀ��

 ��ͼ��ʾ����֪��ABC�У���C=90�㣬AB=5cm��AC=3cm��BC=4cm��AD�ǡ�CAB��ƽ���ߣ���BC����D��DE��AB��E����
��ͼ��ʾ����֪��ABC�У���C=90�㣬AB=5cm��AC=3cm��BC=4cm��AD�ǡ�CAB��ƽ���ߣ���BC����D��DE��AB��E����

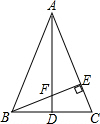 ��ͼ����ABC�У�AB=AC��BE��AC�ڵ�E��AD��BC�ڵ�D����ABE=45�㣬AD��BE���ڵ�F������CF��
��ͼ����ABC�У�AB=AC��BE��AC�ڵ�E��AD��BC�ڵ�D����ABE=45�㣬AD��BE���ڵ�F������CF��