题目内容
17.化简:$\sqrt{{x}^{2}-4x+4}$+$\sqrt{9+6x+{x}^{2}}$(-3<x<2)分析 先利用完全平方公式变形得到原式=$\sqrt{(x-2)^{2}}$+$\sqrt{(x+3)^{2}}$,再利用二次根式的化简得到原式=|x-2|+|x+3|,然后利用x的范围去绝对值,再合并即可.
解答 解:原式=$\sqrt{(x-2)^{2}}$+$\sqrt{(x+3)^{2}}$
=|x-2|+|x+3|,
∵-3<x<2,
∴原式=-(x-2)+x+3
=-x+2+x+3
=5.
点评 本题考查了二次根式的性质与化简:会应用$\sqrt{{a}^{2}}$=|a|进行二次根式的化简.也考查了绝对值的意义.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
20.下列说法中正确的是( )
| A. | 带根号的数都是无理数 | B. | 不带根号的数一定是有理数 | ||
| C. | 无限小数都是无理数 | D. | 无理数是无限小数 |
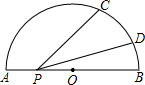 如图,半圆的直径AB=4,P是AB上一动点,C、D在半圆上,$\widehat{BC}$、$\widehat{BD}$的度数分别是75°和15°,则PC+PD的最小值为2$\sqrt{2}$.
如图,半圆的直径AB=4,P是AB上一动点,C、D在半圆上,$\widehat{BC}$、$\widehat{BD}$的度数分别是75°和15°,则PC+PD的最小值为2$\sqrt{2}$.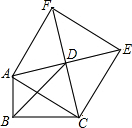 如图,在△ABC中,∠ABC=90°,以AC为一边向三角形外作菱形ACEF,D为菱形ACEF对角线的交点,连接BD,BD平分∠ABC.
如图,在△ABC中,∠ABC=90°,以AC为一边向三角形外作菱形ACEF,D为菱形ACEF对角线的交点,连接BD,BD平分∠ABC.