题目内容
2．
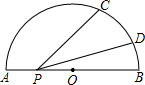如图，半圆的直径AB=4，P是AB上一动点，C、D在半圆上，$\widehat{BC}$、$\widehat{BD}$的度数分别是75°和15°，则PC+PD的最小值为2$\sqrt{2}$．
分析 要求PC+PD的最小值，应先确定点P的位置．作点D关于AB的对称点E，连接CE交AB于点P，则P即是所求作的点，且PC+PD=CE．根据作法知弧CE的度数是90°，即∠COE=90°，作OF⊥CE于F；在Rt△OCF中，∠OCF=45°，OC=2，即可求出CF和CE的长，也就求出了PC+PD的最小值．
解答 解：如图，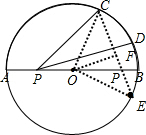
设点D关于AB的对称点为E，连接CE交AB于P，则此时PC+PD的值最小，且PC+PD=PC+PE=CE．连接OC、OE；
∵，$\widehat{BC}$、$\widehat{BD}$的度数分别是75°和15°，
∴弧CD的度数为60°；
∴弧CBE的度数为90°，即∠COE=90°；
过O作OF⊥CE于F，则∠COF=45°；
Rt△OCF中，OC=2，∠COF=45°；
∴CF=$\sqrt{2}$；
∴CE=2CF=2$\sqrt{2}$，即PC+PD的最小值为2$\sqrt{2}$．
故答案为：2$\sqrt{2}$．
点评 此题考查利用轴对称作最短路线，首先正确找到点P的位置，然后根据弧的度数发现特殊三角形，根据垂径定理以及勾股定理进行计算．
练习册系列答案
阅读快车系列答案
相关题目
20．一物体从一高处由静止开始落下，它落下的高度h与时间t有下面的关系：
（1）写出计算物体落下的高度h的公式；
（2）当t=5秒时，物体落下多少米．
| 时间t（s） | 1 | 2 | 3 | 4 | … |
| 高度h（m） | 8×1 | 8×4 | 8×9 | 8×16 | … |
（2）当t=5秒时，物体落下多少米．
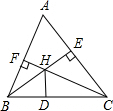如图，在△ABC中，∠ABC=60°，∠ACB=54°，BE是AC边上的高，CF是AB边上的高，H是BE和CF的交点，HD是∠BHC的平分线，求∠ABE，∠ACF和∠CHD的度数．
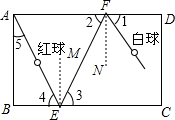如图，选择适当的方向击打白球，可使白球经过两次反弹后将红球撞入底袋，白球在运动过程中，∠1=∠2，∠3=∠4，如果红球与洞口的连线与台球桌边缘的夹角∠5=25°，那么选择∠1是多少度，才能保证红球能直接入袋？为什么？