题目内容
14.若关于x的一元二次方程(k-1)x2-$\sqrt{1-k}$x+$\frac{1}{4}$=0有两个实数根,则k的取值范围是( )| A. | k<1 | B. | k>1 | C. | k≤1 | D. | k≥1 |
分析 由方程是关于x的一元二次方程可得k-1≠0,由$\sqrt{1-k}$有意义可得1-k≥0,由关于x的一元二次方程有两个实数根可得(-$\sqrt{1-k}$)2-4×$\frac{1}{4}$(k-1)≥0,从而可求出k的取值范围.
解答 解:由题可得
$\left\{\begin{array}{l}{k-1≠0}\\{1-k≥0}\\{(-\sqrt{1-k})^{2}-4×\frac{1}{4}(k-1)≥0}\end{array}\right.$,
解得k<1.
故选A.
点评 本题主要考查了一元二次方程的定义、根的判别式、二次根式有意义的条件等知识,本题是一道易错题,容易忽视二次根式有意义的条件.

练习册系列答案
相关题目
9. 如图所示,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象相交于点A(2,6),B(n,-3)两点.请根据图象写出一次函数值大于反比例函数值时x的取值范围-4<x<0或x>2.
如图所示,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象相交于点A(2,6),B(n,-3)两点.请根据图象写出一次函数值大于反比例函数值时x的取值范围-4<x<0或x>2.
 如图所示,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象相交于点A(2,6),B(n,-3)两点.请根据图象写出一次函数值大于反比例函数值时x的取值范围-4<x<0或x>2.
如图所示,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象相交于点A(2,6),B(n,-3)两点.请根据图象写出一次函数值大于反比例函数值时x的取值范围-4<x<0或x>2.
19.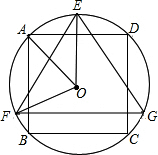 如图,△EFG是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥FG,则∠AOF的度数是( )
如图,△EFG是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥FG,则∠AOF的度数是( )
 如图,△EFG是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥FG,则∠AOF的度数是( )
如图,△EFG是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥FG,则∠AOF的度数是( )| A. | 60° | B. | 65° | C. | 72° | D. | 75° |
4.已知sinA=$\frac{1}{2}$,∠A为锐角,则cos2A等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
 五边形ABCDE的各内角度数如图所示,则x=75.
五边形ABCDE的各内角度数如图所示,则x=75.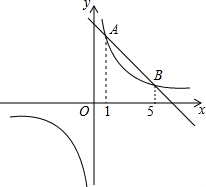 如图,直线y=k1x+b与双曲线y=$\frac{{k}_{2}}{x}$交于A、B两点,它们的横坐标分别为1和5,则不等式k1x<$\frac{{k}_{2}}{x}-b$的解集是0<x<1或x>5.
如图,直线y=k1x+b与双曲线y=$\frac{{k}_{2}}{x}$交于A、B两点,它们的横坐标分别为1和5,则不等式k1x<$\frac{{k}_{2}}{x}-b$的解集是0<x<1或x>5.