题目内容
某空调销售点今年三月份的销售额为60万元,四月份组织了一次宣传活动,销售额上涨了20%,五月份加大了宣传力度,到了六月份,销售额猛增到了112.5万元,求销售点五、六月份平均每月销售额的增长率.
考点:一元二次方程的应用
专题:增长率问题
分析:因为销售点今年三月份的销售额为60万元,四月份销售额上涨了20%,即60(1+20%)万元,后来五月份加大了宣传力度,到了六月份,销售额猛增到了112.5万元,所以可设五、六月份平均每月增长的百分率是x,则六月份的销售额是60(1+20%)(1+x)2,即可列出方程,解之即可求出答案.
解答:解:设五、六月份平均每月增长的百分率为x,则:
60(1+20%)(1+x)2=112.5,
解得x1=0.25=25%,x2=-2.25(不合题意,舍去).
答:五、六月份平均每月增长的百分率是25%.
60(1+20%)(1+x)2=112.5,
解得x1=0.25=25%,x2=-2.25(不合题意,舍去).
答:五、六月份平均每月增长的百分率是25%.
点评:此题结合空调销售点的经营管理与销售额的增减问题,考查了一元二次方程的应用,解题时要注意以下问题:
(1)下降与上升的起点不同:销售额上涨了20%是以三月份的销售额为基础;月销售额上升,是以四月份的销售额为基础;
(2)由于是求五、六月份平均每月增长的百分率,所以可以用平均增长率的数学模型列方程解答.
(1)下降与上升的起点不同:销售额上涨了20%是以三月份的销售额为基础;月销售额上升,是以四月份的销售额为基础;
(2)由于是求五、六月份平均每月增长的百分率,所以可以用平均增长率的数学模型列方程解答.

练习册系列答案
相关题目
长方形周长为30,设长为x,宽为y,则y与x的函数关系式为( )
| A、y=30-x |
| B、y=30-2x |
| C、y=15-x |
| D、y=15+2x |
在下列以线段a,b,c的长三边的三角形中,不能构成直角三角形的是( )
| A、a=9,b=41,c=40 | ||
B、a=b=5,c=5
| ||
| C、a:b:c=5:12:13 | ||
| D、a=10,b=12,c=15 |
 如图,在梯形ABCD中,AD∥BC,对角线AC⊥BD,且AC=12,BD=5,则该梯形的面积是( )
如图,在梯形ABCD中,AD∥BC,对角线AC⊥BD,且AC=12,BD=5,则该梯形的面积是( )| A、30 | ||
| B、15 | ||
C、
| ||
| D、60 |
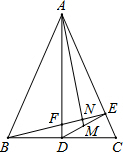 如图,在△ABC中,AB=AC,AD⊥BC于点D,DE⊥AC于点E,M为DE中点,AM与BE相交于点N,AD与BE相交于点F.求证:
如图,在△ABC中,AB=AC,AD⊥BC于点D,DE⊥AC于点E,M为DE中点,AM与BE相交于点N,AD与BE相交于点F.求证: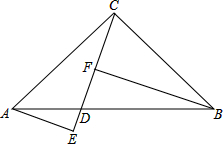 已知,在△ABC中,CA=CB,∠C=90°,D为AB上任意一点,AE⊥CD,垂足为E,BF⊥CD,垂足为F,求证:EF=|AE-BF|.
已知,在△ABC中,CA=CB,∠C=90°,D为AB上任意一点,AE⊥CD,垂足为E,BF⊥CD,垂足为F,求证:EF=|AE-BF|.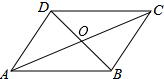 如图,在四边形ABCD中,BC=12,OA=OC=13,BD=10,∠CBD=90°,求证:四边形ABCD为平行四边形.
如图,在四边形ABCD中,BC=12,OA=OC=13,BD=10,∠CBD=90°,求证:四边形ABCD为平行四边形.