题目内容
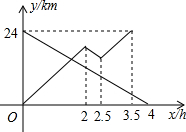 甲船从A港出发顺流匀速驶向B港,行至某处,发现船上一救生圈不知何时落入水中,立刻原路返回,找到救生圈后(寻找时间不计),继续顺流驶向B港.乙船从B港出发逆流匀速驶向A港.已知救生圈漂流速度与水流速度相同;甲、乙两船在静水中的速度相同.甲、乙两船到A港的距离y1、y2(km)与行驶时间x(h)之间的函数图象如图所示.则甲船顺流速度
甲船从A港出发顺流匀速驶向B港,行至某处,发现船上一救生圈不知何时落入水中,立刻原路返回,找到救生圈后(寻找时间不计),继续顺流驶向B港.乙船从B港出发逆流匀速驶向A港.已知救生圈漂流速度与水流速度相同;甲、乙两船在静水中的速度相同.甲、乙两船到A港的距离y1、y2(km)与行驶时间x(h)之间的函数图象如图所示.则甲船顺流速度考点:一次函数的应用
专题:
分析:根据观察图象,可得乙船逆流行驶的速度,根据逆流行驶时,甲乙的速度相同,可得甲逆流行驶的路程,再根据甲顺溜行驶的路程,可得答案.
解答:解:设甲船顺流的速度为akm/h,
乙船在逆流中行驶的速度为24÷4=6(km/h)
甲船在逆流中行驶的速度为6km/h,
甲船在逆流中行驶的路程为6×(2.5-2)=3(km)
由图象得2a-3+(3.5-2.5)a=24,
解得a=9km/h,
故答案为:9.
乙船在逆流中行驶的速度为24÷4=6(km/h)
甲船在逆流中行驶的速度为6km/h,
甲船在逆流中行驶的路程为6×(2.5-2)=3(km)
由图象得2a-3+(3.5-2.5)a=24,
解得a=9km/h,
故答案为:9.
点评:本题考查了一次函数的应用,先由乙的速度,得出甲逆流时的速度是解题关键.

练习册系列答案
相关题目
如果(am•b•bn)3=a6b15,那么m,n的值分别是( )
| A、2,4 | B、2,5 |
| C、3,5 | D、3,-5 |
 如图,直线AB,CD交于点O,射线OM平分∠AOC,若∠BOD=76°,则∠COM=
如图,直线AB,CD交于点O,射线OM平分∠AOC,若∠BOD=76°,则∠COM= 如图5,A为反比例函数y=
如图5,A为反比例函数y=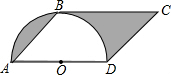 如图,已知?ABCD中,∠A=45°,AD=4cm,以AD为直径的半圆O与BC相切于点B,则图中阴影部分的面积是
如图,已知?ABCD中,∠A=45°,AD=4cm,以AD为直径的半圆O与BC相切于点B,则图中阴影部分的面积是