题目内容
我们把四边形两条对角线中点的连线段称为奇异中位线.现有两个全等三角形,边长分别为3cm,4cm,5cm.将这两个三角形相等的边重合拼成凸四边形,如果凸四边形的奇异中位线的长不为0,那么奇异中位线的长是 cm.
考点:三角形中位线定理,全等三角形的性质
专题:新定义
分析:首先利用勾股定理的逆定理得出边长分别为3cm,4cm,5cm的三角形是直角三角形,然后将这两个直角三角形相等的边重合拼成凸四边形,如果凸四边形的奇异中位线的长不为0,那么只有一种情况,画出图形,根据正弦函数的定义求出OA,由中点的定义得出AM,再根据OM=AM-OA即可求解.
解答: 解:∵32+42=9+16=25=52,
解:∵32+42=9+16=25=52,
∴边长分别为3cm,4cm,5cm的三角形是直角三角形.
如图,将两个全等的直角△ABC与△DEF的斜边AC与DF重合,拼成凸四边形ABCE,AC与BE交于点O,M为AC的中点.
∵△ABC≌△DEF,
∴AB=AE=3cm,∠BAC=∠EDF,
∴BO=OE,AO⊥BE.
在Rt△AOB中,∵∠AOB=90°,
∴OA=AB•cos∠BAO=3×
=
,
∵AM=
AC=
,
∴OM=AM-OA=
-
=
.
即奇异中位线的长是
cm.
故答案为
.
 解:∵32+42=9+16=25=52,
解:∵32+42=9+16=25=52,∴边长分别为3cm,4cm,5cm的三角形是直角三角形.
如图,将两个全等的直角△ABC与△DEF的斜边AC与DF重合,拼成凸四边形ABCE,AC与BE交于点O,M为AC的中点.
∵△ABC≌△DEF,
∴AB=AE=3cm,∠BAC=∠EDF,
∴BO=OE,AO⊥BE.
在Rt△AOB中,∵∠AOB=90°,
∴OA=AB•cos∠BAO=3×
| 3 |
| 5 |
| 9 |
| 5 |
∵AM=
| 1 |
| 2 |
| 5 |
| 2 |
∴OM=AM-OA=
| 5 |
| 2 |
| 9 |
| 5 |
| 7 |
| 10 |
即奇异中位线的长是
| 7 |
| 10 |
故答案为
| 7 |
| 10 |
点评:本题考查了勾股定理的逆定理,图形的拼组,等腰三角形的性质,锐角三角函数的定义,难度适中.根据题目要求画出符合题意的图形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
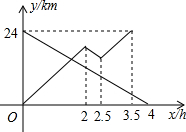 甲船从A港出发顺流匀速驶向B港,行至某处,发现船上一救生圈不知何时落入水中,立刻原路返回,找到救生圈后(寻找时间不计),继续顺流驶向B港.乙船从B港出发逆流匀速驶向A港.已知救生圈漂流速度与水流速度相同;甲、乙两船在静水中的速度相同.甲、乙两船到A港的距离y1、y2(km)与行驶时间x(h)之间的函数图象如图所示.则甲船顺流速度
甲船从A港出发顺流匀速驶向B港,行至某处,发现船上一救生圈不知何时落入水中,立刻原路返回,找到救生圈后(寻找时间不计),继续顺流驶向B港.乙船从B港出发逆流匀速驶向A港.已知救生圈漂流速度与水流速度相同;甲、乙两船在静水中的速度相同.甲、乙两船到A港的距离y1、y2(km)与行驶时间x(h)之间的函数图象如图所示.则甲船顺流速度 如图,平行四边形ABCD中,AE、DF分别是∠BAD、∠ADC的角平分线,相交于点G,交BC边于E、F点,已知AD=8,EF=2,则平行四边形AB长为( )
如图,平行四边形ABCD中,AE、DF分别是∠BAD、∠ADC的角平分线,相交于点G,交BC边于E、F点,已知AD=8,EF=2,则平行四边形AB长为( )