题目内容
在平面直角坐标中,点A(0,3),点B的纵坐标为2,点C的纵坐标为0,当A,B,C三点围成等腰直角三角形时,求点B,C的坐标.
考点:全等三角形的判定与性质,坐标与图形性质,等腰直角三角形
专题:
分析:根据题意,B和C不能作为等腰直角三角形的顶点,画出符合条件的两种情况:过A作直线EF⊥y轴,过C作CM⊥EF于M,作BN⊥EF于N证△AMC≌△BNA,根据全等三角形的性质得出AN=CM=3,OC=AM=BN=1,即可得出答案.
解答:解:根据题意:B和C不能作为等腰直角三角形的顶点,
有两种情况:①如图1所示:

B在y轴的右边,C在x轴的负半轴上,
当A为直角顶点时,AC⊥AB,过A作直线EF⊥y轴,过C作CM⊥EF于M,作BN⊥EF于N,
∵点A(0,3),点B的纵坐标为2,
∴CM=3,BN=3-2=1,
则∠BNA=∠CMA=∠CAB=90°,
所以∠CAM+∠MCA=90°,∠CAM+∠NAB=90°,
所以∠MCA=∠NAB,
在△AMC和△BNA中,
,
∴△AMC≌△BNA(AAS),
∴AN=CM=3,OC=AM=BN=1,
即此时B的坐标是(3,2),C的坐标是(-1,0);
②如图2所示:

B在y轴的左边,C在x轴的正半轴上,
当A为直角顶点时,AC⊥AB,过A作直线EF⊥y轴,过C作CM⊥EF于M,作BN⊥EF于N,
∵点A(0,3),点B的纵坐标为2,
∴CM=3,BN=3-2=1,
则∠BNA=∠CMA=∠CAB=90°,
所以∠CAM+∠MCA=90°,∠CAM+∠NAB=90°,
所以∠MCA=∠NAB,
在△AMC和△BNA中,
,
∴△AMC≌△BNA(AAS),
∴AN=CM=3,OC=AM=BN=1,
即此时B的坐标是(-3,2),C的坐标是(1,0).
所以B(3,2)C(-1,0)或B(-3,2)C(1,0).
有两种情况:①如图1所示:

B在y轴的右边,C在x轴的负半轴上,
当A为直角顶点时,AC⊥AB,过A作直线EF⊥y轴,过C作CM⊥EF于M,作BN⊥EF于N,
∵点A(0,3),点B的纵坐标为2,
∴CM=3,BN=3-2=1,
则∠BNA=∠CMA=∠CAB=90°,
所以∠CAM+∠MCA=90°,∠CAM+∠NAB=90°,
所以∠MCA=∠NAB,
在△AMC和△BNA中,
|
∴△AMC≌△BNA(AAS),
∴AN=CM=3,OC=AM=BN=1,
即此时B的坐标是(3,2),C的坐标是(-1,0);
②如图2所示:

B在y轴的左边,C在x轴的正半轴上,
当A为直角顶点时,AC⊥AB,过A作直线EF⊥y轴,过C作CM⊥EF于M,作BN⊥EF于N,
∵点A(0,3),点B的纵坐标为2,
∴CM=3,BN=3-2=1,
则∠BNA=∠CMA=∠CAB=90°,
所以∠CAM+∠MCA=90°,∠CAM+∠NAB=90°,
所以∠MCA=∠NAB,
在△AMC和△BNA中,
|
∴△AMC≌△BNA(AAS),
∴AN=CM=3,OC=AM=BN=1,
即此时B的坐标是(-3,2),C的坐标是(1,0).
所以B(3,2)C(-1,0)或B(-3,2)C(1,0).
点评:本题考查了等腰直角三角形的性质,坐标与图形性质,全等三角形的性质和判定的应用,用了分类讨论思想,能求出所以情况是解此题的关键,题目比较好,有一定的难度.

练习册系列答案
相关题目
向上发射一枚炮弹,经x秒后的高度为y,且时间与高度的关系式为y=ax2+bx,若此时炮弹在第7秒与第13秒时的高度相等,则在下列哪一个时间的高度是最高的( )
| A、第8秒 | B、第10秒 |
| C、第12秒 | D、第15秒 |
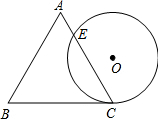 一个边长为2cm的等边△ABC与⊙O等高,如图放置,⊙O与BC相切于点C,⊙O与AC相交于点E,则CE的长为
一个边长为2cm的等边△ABC与⊙O等高,如图放置,⊙O与BC相切于点C,⊙O与AC相交于点E,则CE的长为 如图所示,在Rt△ABC中,∠C=90°,BE是∠ABC的平分线,ED是AB边的垂直平分线.求∠A的度数.
如图所示,在Rt△ABC中,∠C=90°,BE是∠ABC的平分线,ED是AB边的垂直平分线.求∠A的度数. 如图,DO⊥AB于,CO⊥EO于O,则∠AOC与∠BOE的关系是
如图,DO⊥AB于,CO⊥EO于O,则∠AOC与∠BOE的关系是