题目内容
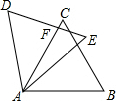
18. 如图,△ABC中,点E,点F在边AB,AC上,且EF∥BC,延长FE至点G,使GE=EF,连接CG交AB于点H.
如图,△ABC中,点E,点F在边AB,AC上,且EF∥BC,延长FE至点G,使GE=EF,连接CG交AB于点H.求证:AE•BH=AB•EH.
分析 由平行线证出△AEF∽△ABC,△EGH∽△BCH,根据相似三角形的对应边的比相等,以及DE=EF即可证得结论.
解答 证明:∵EF∥BC,
∴△AEF∽△ABC,△EGH∽△BCH,
∴$\frac{EF}{BC}=\frac{AE}{AB}$,$\frac{GE}{BC}=\frac{EH}{BH}$,
∵GE=EF,
∴$\frac{AE}{AB}=\frac{EH}{BH}$,
∴AE•BH=AB•EH.
点评 本题考查了相似三角形的判定与性质;由相似三角形的性质得出比例式是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10. 如图所示,转盘被等分成五个扇形,并在上面依次写上数字1,2,3,4,5,若自由转动转盘,当它停止转动时,指针指向奇数区域的概率是( )
如图所示,转盘被等分成五个扇形,并在上面依次写上数字1,2,3,4,5,若自由转动转盘,当它停止转动时,指针指向奇数区域的概率是( )
 如图所示,转盘被等分成五个扇形,并在上面依次写上数字1,2,3,4,5,若自由转动转盘,当它停止转动时,指针指向奇数区域的概率是( )
如图所示,转盘被等分成五个扇形,并在上面依次写上数字1,2,3,4,5,若自由转动转盘,当它停止转动时,指针指向奇数区域的概率是( )| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{5}$ |
7.下列说法正确的是( )
| A. | 某个对象出现的次数称为频率 | |
| B. | 要了解某品牌运动鞋使用寿命可用普查 | |
| C. | 没有水分种子发芽是随机事件 | |
| D. | 折线统计图用于表示数据变化的特征和趋势 |
 电力公司为鼓励市民节约用电,采取按月用电量分段收费的办法,已知某户居民每月应缴电费y(元)与用电量x(度)的函数图象是一条折线(如图所示),根据图象解答下列问题.
电力公司为鼓励市民节约用电,采取按月用电量分段收费的办法,已知某户居民每月应缴电费y(元)与用电量x(度)的函数图象是一条折线(如图所示),根据图象解答下列问题.
 如图,将边长为6的等边三角形ABC绕点A逆时针旋转30度后得到△AED,边AC与DE交于点F,则AF的长为3$\sqrt{3}$.
如图,将边长为6的等边三角形ABC绕点A逆时针旋转30度后得到△AED,边AC与DE交于点F,则AF的长为3$\sqrt{3}$. 如图,△ABC是等腰直角三角形,AC=4,直线l垂直平分AC交AC于点D,点P在直线l上,求△APB的周长的最小值4+4$\sqrt{2}$.
如图,△ABC是等腰直角三角形,AC=4,直线l垂直平分AC交AC于点D,点P在直线l上,求△APB的周长的最小值4+4$\sqrt{2}$. 如图,在平行四边形ABCD中,E为边CD上一点,连结AE,BD,交点为F,若S△DEF:S△BAF=9:64,求:DE:EC的值.
如图,在平行四边形ABCD中,E为边CD上一点,连结AE,BD,交点为F,若S△DEF:S△BAF=9:64,求:DE:EC的值.