题目内容
在Rt△ABC中,∠ACB=90°,∠B=30°,BC=4,以点C为圆心、2cm的长为半径作圆.求证:直线AB与⊙C相切.
考点:切线的判定
专题:
分析:过C作CD⊥AB,垂足为D,则可求得CD=2=半径,可得AB与⊙C相切.
解答: 证明:过C作CD⊥AB,垂足为D,
证明:过C作CD⊥AB,垂足为D,
∵∠ACB=90°,∠B=30°,BC=4,
∴CD=
BC=2,
即点C到直线AB的距离为2cm,
∴直线AB与⊙C相切.
 证明:过C作CD⊥AB,垂足为D,
证明:过C作CD⊥AB,垂足为D,∵∠ACB=90°,∠B=30°,BC=4,
∴CD=
| 1 |
| 2 |
即点C到直线AB的距离为2cm,
∴直线AB与⊙C相切.
点评:本题主要考查切线的判定,掌握切线的判定方法是解题的关键.当有切点时连接圆心和切点,证明该半径与直线垂直;当没有切点时作出圆心到直线的距离,证明该距离与半径相等.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
 由半圆和直角三角形组成的图形,如图,空白部分面积等于(π取3.14,精确到0.1)( )
由半圆和直角三角形组成的图形,如图,空白部分面积等于(π取3.14,精确到0.1)( )| A、15.0 | B、15.1 |
| C、15.2 | D、15.3 |
太阳与地球的距离大约是150000000千米,其中150000000可用科学记数法表示,下列正确的是( )
| A、15×107 |
| B、0.15×109 |
| C、1.5×108 |
| D、1.5亿 |
一元二次方程(3x-1)(-x+1)=3x-1的解是( )
| A、x=0 | ||
| B、x=1 | ||
C、x=
| ||
D、x=
|
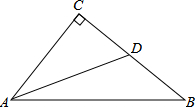 已知在△ABC中,∠C=90°,D点在BC边上,且BD=
已知在△ABC中,∠C=90°,D点在BC边上,且BD= 如图抛物线y=ax2+bx+c与x轴交于点(-3,0)、(2,0),与y轴交于点(0,-3),结合图象回答.
如图抛物线y=ax2+bx+c与x轴交于点(-3,0)、(2,0),与y轴交于点(0,-3),结合图象回答.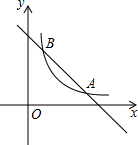 如图,直线y=-x+5与双曲线y=
如图,直线y=-x+5与双曲线y=