题目内容
4.我市某中学今年年初开学后打算招聘一名数学老师,对三名前来应聘的数学老师A、B、C进行了考核,他们的笔试成绩和说课成绩(单位:分)分别用了两种方式进行了统计,如表和图1,| A | B | C | |
| 笔试 | 85 | 95 | 90 |
| 说课 | 90 | 80 | 85 |
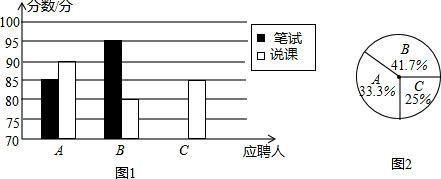
(1)请将表和图1的空缺部分补充完整;
(2)应聘的最后一个程序是由该校的24名数学教师进行投票,三位应聘者的得票情况如图2(没有弃权票,该校的每位教师只能选一位应聘教师),请计算每人的得票数(得票数可是整数哟)
(3)若每票计1分,该校将笔试、说课、得票三项测试得分按3:4:3的比例确定个人成绩,请计算三位应聘者的最后成绩,并根据成绩判断谁能应聘成功.
分析 (1)根据条形统计图找出A的说课成绩,填写表格即可;找出C的笔试成绩,补全条形统计图即可;
(2)由24分别乘以扇形统计图中各学生的百分数即可得到各自的得分;
(3)分别求出三位应聘人的成绩,判断即可.
解答 解:(1)由条形统计图得:A同学的说课成绩为90.填表如下:
| A | B | C | |
| 笔试 | 85 | 95 | 90 |
| 说课 | 90 | 80 | 85 |

故答案为90;
(2)三名同学得票情况是,A:24×33.3%=7.992,
B:24×41.7%=10.008,
C:24×25%=6.
根据实际意义可得,A得8票,B得10票,C得6票;
(3)由题可得,A的最后成绩为:85×$\frac{3}{10}$+90×$\frac{4}{10}$+8×$\frac{3}{10}$=63.9,
B的最后成绩为:95×$\frac{3}{10}$+80×$\frac{4}{10}$+10×$\frac{3}{10}$=63.5,
C的最后成绩为:90×$\frac{3}{10}$+85×$\frac{4}{10}$+6×$\frac{3}{10}$=62.8,
所以A能应聘成功.
点评 本题考查的是条形统计图与扇形统计图的综合运用.读懂统计图,从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据.扇形统计图可以很清楚地表示出各部分数量同总数之间的关系.也考查了加权平均数.

练习册系列答案
相关题目
20.下列图形中不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
9.为了调查居民的生活水平,有关部门对某居委会的50户居民的家庭存款额进行了调查,数据(单位:万元)如下:
1.7 3.5 2.3 6.4 2.0 1.9 6.7 4.8 5.0 4.7
2.3 3.4 5.6 3.7 2.2 3.3 5.8 4.3 3.6 3.8
3.0 5.1 7.0 3.1 2.9 4.9 5.8 3.6 3.0 4.2
4.0 3.9 5.1 6.3 1.8 3.2 5.1 5.7 3.9 3.1
2.5 2.8 4.5 4.9 5.3 2.6 7.2 1.9 5.0 3.8
(1)这50个家庭存款额的最大值、最小值分别是多少?它们相差多少?
(2)填表:
(3)根据上表谈谈这50户家庭存款额的分布情况.
1.7 3.5 2.3 6.4 2.0 1.9 6.7 4.8 5.0 4.7
2.3 3.4 5.6 3.7 2.2 3.3 5.8 4.3 3.6 3.8
3.0 5.1 7.0 3.1 2.9 4.9 5.8 3.6 3.0 4.2
4.0 3.9 5.1 6.3 1.8 3.2 5.1 5.7 3.9 3.1
2.5 2.8 4.5 4.9 5.3 2.6 7.2 1.9 5.0 3.8
(1)这50个家庭存款额的最大值、最小值分别是多少?它们相差多少?
(2)填表:
| 存款额x(万元) | 划记 | 户数 |
| 1.0≤x<2.0 | 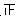 | 4 |
| 2.0≤x<3.0 | 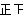 | 8 |
| 3.0≤x<4.0 | 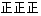 | 15 |
| 4.0≤x<5.0 | 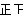 | 8 |
| 5.0≤x<6.0 | 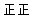 | 10 |
| 6.0≤x<7.0 | 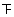 | 3 |
| 7.0≤x<8.0 |  | 2 |
 如图,在△ABC中,AB=AC,D为AC上的一点,求证:AC>$\frac{1}{2}$(BD+CD).
如图,在△ABC中,AB=AC,D为AC上的一点,求证:AC>$\frac{1}{2}$(BD+CD).
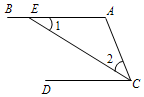 请将下列证明过程补充完整:
请将下列证明过程补充完整: