题目内容
 如图所示,把一底角为45°的等腰梯形放在平面直角坐标系中,已知梯形腰长为2
如图所示,把一底角为45°的等腰梯形放在平面直角坐标系中,已知梯形腰长为2| 2 |
考点:等腰梯形的性质,坐标与图形性质
专题:
分析:过A作AM⊥OC于M,过B作BN⊥OC于N,得出平行四边形AMNB,推出MN=AB=2,求出AM=2,求出OM=MN=CN=2,即可得出答案.
解答:解:
过A作AM⊥OC于M,过B作BN⊥OC于N,
则AM∥BN,
∵AB∥OC,
∴四边形AMNB是平行四边形,
∴AB=MN=2,AM=BN,
∵四边形OABC是等腰梯形,
∴OM=ON,
∵AB=2
,∠AOC=45°,
∴AM=OA×sin45°=2
×
=2,
∴OM=AM=2,
∴OC=2+2+2=6,BN=AM=2,
∴A(2,2),B(4,2),C(6,0).

过A作AM⊥OC于M,过B作BN⊥OC于N,
则AM∥BN,
∵AB∥OC,
∴四边形AMNB是平行四边形,
∴AB=MN=2,AM=BN,
∵四边形OABC是等腰梯形,
∴OM=ON,
∵AB=2
| 2 |
∴AM=OA×sin45°=2
| 2 |
| ||
| 2 |
∴OM=AM=2,
∴OC=2+2+2=6,BN=AM=2,
∴A(2,2),B(4,2),C(6,0).
点评:本题考查了等腰梯形,解直角三角形,平行四边形的性质和判定的应用,解此题的关键是正确作辅助线,题目比较好,难度适中.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若关于x的方程(m-2)x2+
x+1=0是一元二次方程,则m的取值范围是( )
| m |
| A、m≠2 | B、m>0 |
| C、m≠2且m≥0 | D、m为任何实数 |
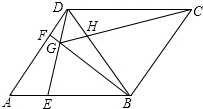 如图,在菱形ABCD中,AB=BD.点E、F分别在AB、AD上,且AE=DF.连接BF与DE相交于点G,连接CG.
如图,在菱形ABCD中,AB=BD.点E、F分别在AB、AD上,且AE=DF.连接BF与DE相交于点G,连接CG.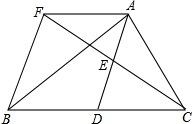 如图,在△ABC中,D是BC边的中点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,连接BF.
如图,在△ABC中,D是BC边的中点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,连接BF. 数形结合是一种重要的数学思想,认真观察图形,然后完成下列问题:
数形结合是一种重要的数学思想,认真观察图形,然后完成下列问题: 如图,四边形ABCD是平行四边形,点E、F是四边形ABCD的对角线AC上的两点,DF∥BE.求证:AE=CF.
如图,四边形ABCD是平行四边形,点E、F是四边形ABCD的对角线AC上的两点,DF∥BE.求证:AE=CF.