题目内容
5. 如图,△ABC中,AB=10,AC=7,AD平分∠BAC,AE是BC边上的中线,过点C作CG⊥AD于F,交AB于G,连接EF,则线段EF的长为1.5.
如图,△ABC中,AB=10,AC=7,AD平分∠BAC,AE是BC边上的中线,过点C作CG⊥AD于F,交AB于G,连接EF,则线段EF的长为1.5.
分析 首先证明△AGF≌△ACF,则AG=AC=4,GF=CF,证明EF是△BCG的中位线,利用三角形的中位线定理即可求解.
解答 解:∵AD平分∠BAC,
∴∠GAF=∠CAF,
∵CG⊥AD,
∴∠AFG=∠AFC,
在△AGF和△ACF中,$\left\{\begin{array}{l}{∠GAF=∠CAF}&{\;}\\{AF=AF}&{\;}\\{∠AFG=∠AFC}&{\;}\end{array}\right.$,
∴△AGF≌△ACF(ASA),
∴AG=AC=6,GF=CF,
则BG=AB-AG=10-7=3.
又∵BE=CE,
∴EF是△BCG的中位线,
∴EF=$\frac{1}{2}$BG=1.5.
故答案是:1.5.
点评 本题考查了全等三角形的判定以及三角形的中位线定理,证明三角形全等是解决问题的突破口.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图∠AED=∠C,∠DEF=∠B,试说明∠1+∠2=180°.
如图∠AED=∠C,∠DEF=∠B,试说明∠1+∠2=180°. 如图,在△ABC中,点D、E分别在边AB、AC上,$\frac{AD}{AC}$=$\frac{AE}{AB}$,∠BAC的平分线AG分别交线段DE、BC于点F、G.
如图,在△ABC中,点D、E分别在边AB、AC上,$\frac{AD}{AC}$=$\frac{AE}{AB}$,∠BAC的平分线AG分别交线段DE、BC于点F、G.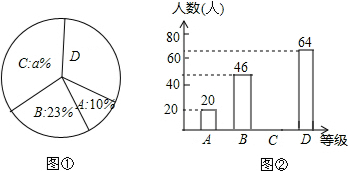 一家公司对一种新研发的手机进行市场问卷调查,其中一个项目是让每个人按A(不喜欢)、B(一般)、C(比较喜欢)、D(非常喜欢)四个等级对该手机进行评价,图①和图②是该公司采集数据后,绘制的两幅不完整的统计图,请你根据以上统计图提供的信息,回答下列问题:
一家公司对一种新研发的手机进行市场问卷调查,其中一个项目是让每个人按A(不喜欢)、B(一般)、C(比较喜欢)、D(非常喜欢)四个等级对该手机进行评价,图①和图②是该公司采集数据后,绘制的两幅不完整的统计图,请你根据以上统计图提供的信息,回答下列问题: