题目内容
10.当m=-5时,分式(m+2-$\frac{5}{m-2}$)•$\frac{2m-4}{3-m}$的值是4.分析 将计算括号内分式的加法,再计算乘法即可化简原式,最后代入化简后的式子即可得答案.
解答 解:原式=$\frac{{m}^{2}-4-5}{(m-2)}$•$\frac{2(m-2)}{-(m-3)}$
=$\frac{(m+3)(m-3)}{m-2}$•$\frac{2(m-2)}{-(m-3)}$
=-2(m+3),
当m=-5时,原式=-2×(-5+3)=-2×(-2)=4,
故答案为:4.
点评 本题主要考查分式的化简求值和代数式的求值及实数的运算,在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.下列命题中是真命题的是( )
| A. | 所有的矩形都相似 | |
| B. | 所有的直角三角形都相似 | |
| C. | 有一个角是50°的所有等腰三角形都相似 | |
| D. | 有一个角是100°的所有等腰三角形都相似 |
18.计算-0.32÷0.5×2÷(-2)3的结果是( )
| A. | $\frac{9}{100}$ | B. | -$\frac{9}{100}$ | C. | $\frac{9}{200}$ | D. | -$\frac{9}{200}$ |
2.下列解方程过程中,变形正确的是( )
| A. | 由2x-1=3得2x=3-1 | |
| B. | 由$\frac{x}{3}$-$\frac{x}{2}$=1得2x-3x=6 | |
| C. | 由-5x=6得x=-$\frac{5}{6}$ | |
| D. | 由$\frac{x}{4}$+1=$\frac{3x+1}{0.1}$+1.2得$\frac{x}{4}$+1=$\frac{3x+1}{1}$+12 |
19.下列计算正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 3$\sqrt{2}$-2$\sqrt{2}$=1 | C. | $\sqrt{24}$÷$\sqrt{6}$=4 | D. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ |
 如图,△ABC中,AB=10,AC=7,AD平分∠BAC,AE是BC边上的中线,过点C作CG⊥AD于F,交AB于G,连接EF,则线段EF的长为1.5.
如图,△ABC中,AB=10,AC=7,AD平分∠BAC,AE是BC边上的中线,过点C作CG⊥AD于F,交AB于G,连接EF,则线段EF的长为1.5.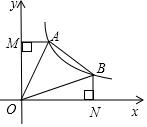 如图,直线y=-x+b(b>0)与双曲线y=$\frac{k}{x}$(x>0)交于A、B两点,连接OA、OB,AM⊥y轴于M,BN⊥x轴于N,现有以下结论:
如图,直线y=-x+b(b>0)与双曲线y=$\frac{k}{x}$(x>0)交于A、B两点,连接OA、OB,AM⊥y轴于M,BN⊥x轴于N,现有以下结论: 如图,在扇形AOB中,∠AOB=45°,点C为OB的中点,以点C为圆心,以OC的长为半径画半圆交OA于点D,若OB=2,则阴影部分的面积为$\frac{π}{4}$-$\frac{1}{2}$.
如图,在扇形AOB中,∠AOB=45°,点C为OB的中点,以点C为圆心,以OC的长为半径画半圆交OA于点D,若OB=2,则阴影部分的面积为$\frac{π}{4}$-$\frac{1}{2}$.