题目内容
平面内的两条直线有相交和平行两种位置关系,下面我们就来研究其中的几种位置关系中角所存在的几种数量关系.
(1)问题探究1:
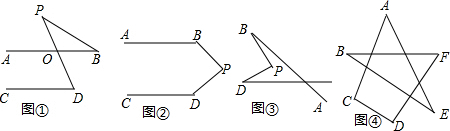
如图①,若AB∥CD,点P在AB、CD外部,则有∠D=∠BOD,又因为∠BOD是△POB的外角,故∠BOD=∠BPD+∠B,得∠BPD=∠D-∠B.将点P移到AB、CD内部,如图②,以上结论是否成立?若成立,说明理由;若不成立,则∠BPD、∠B、∠D之间有何数量关系?请证明你的结论;
(2)问题探究2:在图②中,将直线AB绕点B逆时针方向旋转一定角度交直线CD延长线于点Q,如图③,则∠BPD﹑∠B﹑∠PDQ﹑∠BQD之间有何数量关系?请证明你的结论;
(3)根据(2)的结论直接写出图④中∠A+∠B+∠C+∠D+∠E+∠F的度数.
(1)问题探究1:
如图①,若AB∥CD,点P在AB、CD外部,则有∠D=∠BOD,又因为∠BOD是△POB的外角,故∠BOD=∠BPD+∠B,得∠BPD=∠D-∠B.将点P移到AB、CD内部,如图②,以上结论是否成立?若成立,说明理由;若不成立,则∠BPD、∠B、∠D之间有何数量关系?请证明你的结论;
(2)问题探究2:在图②中,将直线AB绕点B逆时针方向旋转一定角度交直线CD延长线于点Q,如图③,则∠BPD﹑∠B﹑∠PDQ﹑∠BQD之间有何数量关系?请证明你的结论;
(3)根据(2)的结论直接写出图④中∠A+∠B+∠C+∠D+∠E+∠F的度数.

考点:平行线的性质
专题:
分析:(1)过点P作PE∥AB,根据平行线的性质可知∠B+∠BPE=180°,∠D+∠EPD=180°,即∠B+∠BPD+∠D=360°.
(2)连接QP并延长至E,根据∠BPE是△BPQ的一个外角,得到∠BPE=∠BQP+∠B.同理得到∠EPD=∠DQP+∠PDQ,从而∠BPD=∠B+∠PDQ+∠BQD.
(3)由(2)得∠A+∠B+∠C+∠D+∠E+∠F=360°.
(2)连接QP并延长至E,根据∠BPE是△BPQ的一个外角,得到∠BPE=∠BQP+∠B.同理得到∠EPD=∠DQP+∠PDQ,从而∠BPD=∠B+∠PDQ+∠BQD.
(3)由(2)得∠A+∠B+∠C+∠D+∠E+∠F=360°.
解答: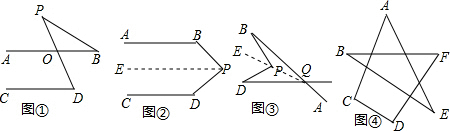 解:(1)上述结论不成立.
解:(1)上述结论不成立.
过点P作PE∥AB
∴∠B+∠BPE=180°,
又∵AB∥CD,
∴PE∥CD,
∴∠D+∠EPD=180°,
∴∠B+∠BPE+∠D+∠EPD=360°,
即∠B+∠BPD+∠D=360°.
(2)∠BPD=∠B+∠PDQ+∠BQD,
连接QP并延长至E,
∵∠BPE是△BPQ的一个外角,
∴∠BPE=∠BQP+∠B.
同理:∠EPD=∠DQP+∠PDQ.
∴∠BPE+∠EPD=∠BQP+∠B+∠DQP+∠PDQ.
即:∠BPD=∠B+∠PDQ+∠BQD.
(3)∠A+∠B+∠C+∠D+∠E+∠F=360°.
 解:(1)上述结论不成立.
解:(1)上述结论不成立.过点P作PE∥AB
∴∠B+∠BPE=180°,
又∵AB∥CD,
∴PE∥CD,
∴∠D+∠EPD=180°,
∴∠B+∠BPE+∠D+∠EPD=360°,
即∠B+∠BPD+∠D=360°.
(2)∠BPD=∠B+∠PDQ+∠BQD,
连接QP并延长至E,
∵∠BPE是△BPQ的一个外角,
∴∠BPE=∠BQP+∠B.
同理:∠EPD=∠DQP+∠PDQ.
∴∠BPE+∠EPD=∠BQP+∠B+∠DQP+∠PDQ.
即:∠BPD=∠B+∠PDQ+∠BQD.
(3)∠A+∠B+∠C+∠D+∠E+∠F=360°.
点评:本题考查了平行线的性质,同时要结合三角外角的性质,最关键的是知道两直线平行,内错角相等.

练习册系列答案
相关题目
下列函数:①y=1-x;②y=2x+11;③y=x2+x+1;④y=
中.是关于x的一次函数的有( )
| 1 |
| x |
| A、4个 | B、3个 | C、2个 | D、1个 |
若三角形两边中垂线的交点在三角形的一边上,则这个三角形为( )
| A、钝角三角形 |
| B、直角三角形 |
| C、锐角三角形 |
| D、等腰三角形 |
若关于x的方程kx-3x=24与
=5的解相同,则k的值为( )
| 2x-1 |
| 3 |
| A、8 | B、6 | C、2 | D、0 |
 某班同学在“献爱心”活动中捐了图书,捐书的情况如下:每人捐书的册数为:5,10,15,20,相应的捐书人数为:17,22,4,2.根据题目中所给的条件回答下列问题:
某班同学在“献爱心”活动中捐了图书,捐书的情况如下:每人捐书的册数为:5,10,15,20,相应的捐书人数为:17,22,4,2.根据题目中所给的条件回答下列问题: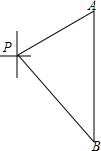 如图,一艘海轮位于灯塔P的北偏东60°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处距离灯塔P有多远?(精确到0.01海里)
如图,一艘海轮位于灯塔P的北偏东60°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处距离灯塔P有多远?(精确到0.01海里)