题目内容
在太阳光下，身高为1.6米的小芳在地面上的影长为2米．当他测量教学楼旁的一棵大树影长时，因大树靠近教学楼，有一部分影子在墙上．经测量，地面部分影长为8.5米，墙上影长为1.2米，那么这棵大树高约多少米？考点：相似三角形的应用
专题：
分析：利用同一时刻太阳下实际物体与影长的关系求出AE的长，即可得出AB的长．
解答：
解：如图所示：过点D作DE⊥AB于点E，
由题意可得：DE=BC=8.5m，DC=BE=1.2m，
∵身高为1.6米的小芳在地面上的影长为2米，
∴
=
，
解得：EA=6.8（m），
故AB=AE+BE=1.2+6.8=8（m），
答：这棵大树高约8米．
解：如图所示：过点D作DE⊥AB于点E，由题意可得：DE=BC=8.5m，DC=BE=1.2m，
∵身高为1.6米的小芳在地面上的影长为2米，
∴
| AE |
| ED |
| 1.6 |
| 2 |
解得：EA=6.8（m），
故AB=AE+BE=1.2+6.8=8（m），
答：这棵大树高约8米．
点评：此题主要考查了相似三角形的应用，正确得出AE的长是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
若三角形两边中垂线的交点在三角形的一边上，则这个三角形为（ ）
| A、钝角三角形 |
| B、直角三角形 |
| C、锐角三角形 |
| D、等腰三角形 |
已知二次函数y=1-3x+5x2，则其二次项系数a，一次项系数b，常数项c分别是（ ）
| A、a=1，b=-3，c=5 |
| B、a=1，b=3，c=5 |
| C、a=5，b=3，c=1 |
| D、a=5，b=-3，c=1 |
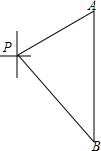如图，一艘海轮位于灯塔P的北偏东60°方向，距离灯塔80海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东45°方向上的B处，这时，海轮所在的B处距离灯塔P有多远？（精确到0.01海里）