题目内容
当x=1时,ax3+bx2+cx-3=9,且a:b:c=1:2:3,那么3a+2b+c= .
考点:解三元一次方程组
专题:
分析:先把x=1代入式子ax3+bx2+cx-3=9得a+b+c=12,设a=k,b=2k,c=3k,代入化简后的式子就可以求出k的值,从而求出a、b、c的值,就可以求出结论.
解答:解:∵x=1时,ax3+bx2+cx-3=9,
∴a+b+c=12.
∵a:b:c=1:2:3,
∴设a=k,b=2k,c=3k,则
∴k+2k+3k=12,
∴k=2,
∴a=2,b=4,c=6,
∴3a+2b+c=3×2+2×4+6=20.
故答案为:20
∴a+b+c=12.
∵a:b:c=1:2:3,
∴设a=k,b=2k,c=3k,则
∴k+2k+3k=12,
∴k=2,
∴a=2,b=4,c=6,
∴3a+2b+c=3×2+2×4+6=20.
故答案为:20
点评:本题考查了参数法在三元一次方程中的运用,三元一次方程组的解法.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
 如图,正△ABC内接于⊙O,动点P在圆周的劣弧AB上,且不与A、B重合,则∠BPC=( )
如图,正△ABC内接于⊙O,动点P在圆周的劣弧AB上,且不与A、B重合,则∠BPC=( )| A、60° | B、30° |
| C、90° | D、120° |
小明手中有三根木棒,长分别为6cm,8cm,10cm,将三根木棒首尾顺次连接,能组成( )三角形.
| A、锐角 | B、直角 |
| C、钝角 | D、以上都有可能 |
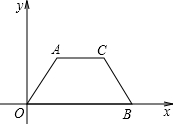 如图所示,梯形AOBC中,AC∥OB,AO=CB,A(2,2
如图所示,梯形AOBC中,AC∥OB,AO=CB,A(2,2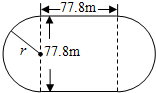
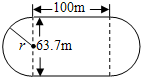

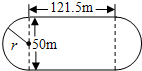
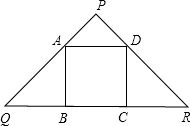 已知正方形ABCD内接于等腰直角三角形PQR,则PA:AQ=
已知正方形ABCD内接于等腰直角三角形PQR,则PA:AQ= 为了测量一个光盘的直径,小明把直尺、光盘和三角尺按图所示放置于桌面上,并量出AB=6cm.这张光盘的直径是多少?
为了测量一个光盘的直径,小明把直尺、光盘和三角尺按图所示放置于桌面上,并量出AB=6cm.这张光盘的直径是多少?