题目内容
18.解方程:(1)3x-2=10-2(x+1);
(2)$\frac{2x+1}{3}-\frac{5x-1}{6}=1$;
(3)$\left\{\begin{array}{l}x+2y=5\\ 3x-2y=-1\end{array}\right.$;
(4)$\left\{\begin{array}{l}2x+y+z=15\\ x+2y+z=16\\ x+y+2z=17\end{array}\right.$.
分析 (1)方程去括号,移项合并,将x系数化为1,即可求出解.
(2)方程去分母,去括号,移项,合并同类项,将x的系数化为1,即可求出方程的解.
(3)解此题运用的是代入消元法.
(4)根据三个方程中同一未知道数的系数相同或互为相反数,应用加减法来解.
解答 解:(1)去括号:3x-2=10-2x-2,
移项,得3x+2x=10-2+2,
合并同类项,得5x=10,
系数化为1,得x=2.
(2)去分母,得2(2x+1)-(5x-1)=6,;
去括号民,得4x+2-5x+1=6,
移项,合并同类项,得-x=3,
系数化为1,得x=-3.
(3)$\left\{\begin{array}{l}x+2y=5\\ 3x-2y=-1\end{array}\right.$;$\underset{\stackrel{①}{\;}}{②}$
①+②,得4x=4,
解,得x=1,
把x=1代入①,得1+2y=5,
解,得y=2,
∴原方程组的解是$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.
(4)$\left\{\begin{array}{l}2x+y+z=15\\ x+2y+z=16\\ x+y+2z=17\end{array}\right.$.$\underset{\stackrel{①}{②}}{③}$
①+②-③,得2x+2y=14,
∴x+y=7 ④,
①-②,得,x-y=-1 ⑤,
方程④⑤组成二元一次方程组$①\left\{\begin{array}{l}{x+y=7}\\{x-y=-1}\end{array}\right.$
解这个方程组,得$\left\{\begin{array}{l}{x=3}\\{y=4}\end{array}\right.$,
把$\left\{\begin{array}{l}{x=3}\\{y=4}\end{array}\right.$代入①,得2×3+4+z=15,
解,得z=5,
∴原方程组的解是$\left\{\begin{array}{l}{x=3}\\{y=4}\\{z=5}\end{array}\right.$
点评 此题考查了(1)解一元一次方程,其步骤为:去分母,去括号,移项合并,将未知数系数化为1,求出解
(2)简单的二(三)元一次方程组的解法的运用和理解,学生可以通过题目的训练达到对知识的强化和运用.

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案| A. |  | B. |  | C. |  | D. |  |
| A. | 等腰三角形 | B. | 锐角三角形 | C. | 钝角三角形 | D. | 直角三角形 |
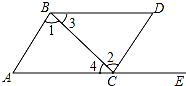 如图,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
如图,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )| A. | ∠3=∠4 | B. | ∠D+∠ACD=180° | C. | ∠D=∠DCE | D. | ∠1=∠2 |
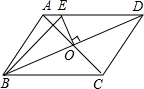 如图,平行四边形ABCD的对角线相交于点O,且AD≠CD,过点O作OE⊥BD,交AD于点E,如果△ABE的周长为4,那么平行四边形ABCD的周长是8.
如图,平行四边形ABCD的对角线相交于点O,且AD≠CD,过点O作OE⊥BD,交AD于点E,如果△ABE的周长为4,那么平行四边形ABCD的周长是8.