题目内容
3.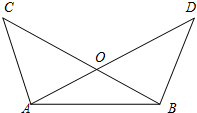 如图所示,∠BAC=∠ABD,AC=BD,点O是AD,BC的交点.
如图所示,∠BAC=∠ABD,AC=BD,点O是AD,BC的交点.(1)求证:∠CBA=∠DAB;
(2)若AD⊥AC,且OA=3,AC=4,求BC的长.
分析 (1)根据SAS推出△ABC≌△BAD,根据全等三角形的性质得出即可;
(2)根据全等得出OB=OA,根据勾股定理求出OC,即可得出答案.
解答 (1)证明:在△ABC和△BAD中,
$\left\{\begin{array}{l}{AC=BD}\\{∠CAB=∠DBA}\\{AB=BA}\end{array}\right.$,
∴△ABC≌△BAD(SAS),
∴∠CBA=∠DAB;
(2)解:∵∠CBA=∠DAB,OA=3,
∴OB=OA=3,
∵AD⊥AC,
∴∠CAO=90°,
∵OA=3,AC=4,
∴由勾股定理得:OC=5,
∴BC=3+5=8.
点评 本题考查了勾股定理,全等三角形的性质和判定的应用,能推出△ABC≌△BAD是解此题的关键.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
11.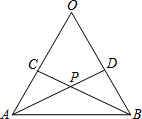 如图所示,AO=BO,CO=DO,连接AD、BC,设AD、BC相交于点P.结论:①△AOD≌△BOC;②△APC≌△BPD;③点P在∠AOB的平分线上.以上结论中( )
如图所示,AO=BO,CO=DO,连接AD、BC,设AD、BC相交于点P.结论:①△AOD≌△BOC;②△APC≌△BPD;③点P在∠AOB的平分线上.以上结论中( )
 如图所示,AO=BO,CO=DO,连接AD、BC,设AD、BC相交于点P.结论:①△AOD≌△BOC;②△APC≌△BPD;③点P在∠AOB的平分线上.以上结论中( )
如图所示,AO=BO,CO=DO,连接AD、BC,设AD、BC相交于点P.结论:①△AOD≌△BOC;②△APC≌△BPD;③点P在∠AOB的平分线上.以上结论中( )| A. | 只有①正确 | B. | 只有②正确 | C. | 只有①②正确 | D. | ①②③都正确 |
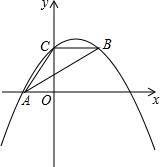 如图,抛物线y=ax2+bx+c经过A(-3.0)、C(0,4),点B在抛物线上,CB∥x轴,且AB平分∠CAO.
如图,抛物线y=ax2+bx+c经过A(-3.0)、C(0,4),点B在抛物线上,CB∥x轴,且AB平分∠CAO.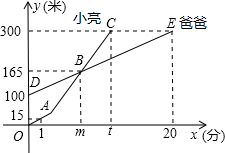 小亮和爸爸登山,两人距离地面的高度y(米)与小亮登山时间x(分)之间的函数图象分别如图中折线OA-AC和线段DE所示,根据函数图象进行以下探究:
小亮和爸爸登山,两人距离地面的高度y(米)与小亮登山时间x(分)之间的函数图象分别如图中折线OA-AC和线段DE所示,根据函数图象进行以下探究: