题目内容
18.已知:在直径是10的⊙O中,$\widehat{AB}$的度数是60°,求弦AB的弦心距.分析 根据题意画出图形,过点O作OD⊥AB于点D,由等腰三角形的性质可得出∠AOD=30°,再根据锐角三角函数的定义即可得出结论.
解答  解:如图,过点O作OD⊥AB于点D,
解:如图,过点O作OD⊥AB于点D,
∵OA=OB,∠AOB=60°,
∴∠AOD=$\frac{1}{2}$∠AOB=30°.
∵⊙O的直径为10,
∴OA=5,
∴OD=OA•cos30°=5×$\frac{\sqrt{3}}{2}$=$\frac{5\sqrt{3}}{2}$.
点评 本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.下列两项中,属于同类项的是( )
| A. | 62与x2 | B. | mn和-mn | C. | 0.2x2y与0.2xy2 | D. | 4ab与4abc |
 如图,在平面直角坐标系中,点A的坐标为(1,3),点B在x轴上,△AOB的面积是3.
如图,在平面直角坐标系中,点A的坐标为(1,3),点B在x轴上,△AOB的面积是3.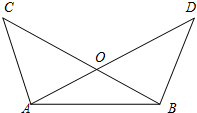 如图所示,∠BAC=∠ABD,AC=BD,点O是AD,BC的交点.
如图所示,∠BAC=∠ABD,AC=BD,点O是AD,BC的交点.
 如图,点C在线段AB上,AC=8cm,CB=6cm,点M、N分别是AC、BC的中点.
如图,点C在线段AB上,AC=8cm,CB=6cm,点M、N分别是AC、BC的中点.