Question

9．半径为2的正六边形的中心角为60，边心距为$\sqrt{3}$，面积为6$\sqrt{3}$．

Answer 1

分析 根据题意画出图形，求出∠AOB的度数，判断出△AOB的形状即可得出正六边形的半径，再作OM⊥AB于点M，利用锐角三角函数的定义求出OM的长，进而可得出结论．

解答 解：如图所示：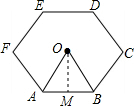
∵六边形ABCDE是正六边形，
∴∠AOB=$\frac{360°}{6}$=60°；
∵OA=OB，
∴△AOB是等边三角形，
∴OA=OB=AB=2；
作OM⊥AB于点M，
∵OA=2，∠OAB=60°，
∴OM=OA•sin60°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$，
∴正六边形的面积为6×$\frac{1}{2}$×2$\sqrt{3}$=6$\sqrt{3}$．
故答案为：60°，$\sqrt{3}$，6$\sqrt{3}$．

点评 此题考查了圆的内接正六边形的性质、正多边形的内角和、等边三角形的判定与性质以及三角函数等知识．此题难度不大，注意掌握数形结合思想的应用．