题目内容
9. 如图,⊙O是等腰直角三角形ACB的内切圆,∠ACB=90°,AC=4,则⊙O的半径等于4-2$\sqrt{2}$.
如图,⊙O是等腰直角三角形ACB的内切圆,∠ACB=90°,AC=4,则⊙O的半径等于4-2$\sqrt{2}$.
分析 由于等腰直角三角形与圆O相内切,所以可设切点为E、F,连接OE、OF,可证明四边形CEOF是正方形,利用切线长定理即可求出圆O的半径.
解答 解:设⊙O与等腰直角三角形相切于E、F、G,连接OE、OF,
∴∠CEO=∠CFO=90°,
又∵∠C=90°,OE=OF,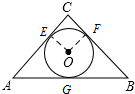
∴四边形CEOF是正方形,
设⊙O的半径为r,
∴CE=CF=r,
∴AE=BF=4-r,
由切线长定理可得:AG=AE=4-r,BG=BF=4-r,
由勾股定理可得:AB=4$\sqrt{2}$,
∴AG+BG=AB,
∴4-r+4-r=4$\sqrt{2}$,
∴r=4-2$\sqrt{2}$,
故答案为:4-2$\sqrt{2}$.
点评 本题考查三角形内切圆的性质,涉及等腰三角形的性质,正方形的判定与性质,勾股定理、切线长定理等知识,综合程度较高,属于中等题型.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
4.用配方法解方程x2-2$\sqrt{2}$x+1=0,则方程可变形为( )
| A. | (x-$\sqrt{2}$)2=1 | B. | (x-$\sqrt{2}$)2=0 | C. | (x-$\sqrt{2}$)2=-1 | D. | (x-$\sqrt{2}$)2=$\sqrt{2}$-1 |
14. 如图,在Rt△ABC中,∠C=90°,∠CAB=60°,边AB的垂直平分线交BC于点D,交AB于点E,若DE=3.8cm,则BC的长等于( )
如图,在Rt△ABC中,∠C=90°,∠CAB=60°,边AB的垂直平分线交BC于点D,交AB于点E,若DE=3.8cm,则BC的长等于( )
 如图,在Rt△ABC中,∠C=90°,∠CAB=60°,边AB的垂直平分线交BC于点D,交AB于点E,若DE=3.8cm,则BC的长等于( )
如图,在Rt△ABC中,∠C=90°,∠CAB=60°,边AB的垂直平分线交BC于点D,交AB于点E,若DE=3.8cm,则BC的长等于( )| A. | 3.8cm | B. | 7.6cm | C. | 11.4cm | D. | 11.2cm |
 如图,正方形ABCD中,点E,F为对角线BD上两点,DE=BF=2cm,EF=4cm,四边形AECF的周长是8$\sqrt{5}$cm.
如图,正方形ABCD中,点E,F为对角线BD上两点,DE=BF=2cm,EF=4cm,四边形AECF的周长是8$\sqrt{5}$cm. 如图,四边形ABCD为正方形,∠AEC=90°,过点E作EF⊥AD交BC于点I,交AD于点F,连接BF交AE于点G,连接CG,交DF=3,AB=5,则tan∠CGE=$\frac{11\sqrt{2}}{24}$.
如图,四边形ABCD为正方形,∠AEC=90°,过点E作EF⊥AD交BC于点I,交AD于点F,连接BF交AE于点G,连接CG,交DF=3,AB=5,则tan∠CGE=$\frac{11\sqrt{2}}{24}$. 如图,正方形ABCD的顶点B、C都在直角坐标系的x轴上,若点D的坐标是(3,4),则点A的坐标是(-1,4).
如图,正方形ABCD的顶点B、C都在直角坐标系的x轴上,若点D的坐标是(3,4),则点A的坐标是(-1,4).