Question

19．如图，正方形ABCD中，点E，F为对角线BD上两点，DE=BF=2cm，EF=4cm，四边形AECF的周长是8$\sqrt{5}$cm．

Answer 1

分析 如图，连接AC交BD于点O，首先证明四边形AECF是菱形，利用勾股定理求出AE即可．

解答 解：如图，连接AC交BD于点O．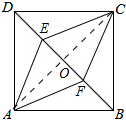

∵四边形ABCD是正方形，
∴OA=OC=OD=OB，AC⊥BD，
∵DE=FB=2，EF=4，
∴OE=OF=2，OA=OC=4，
∴四边形AECF是菱形，∵EF⊥AC，
∴四边形AECF是菱形，
∴AE=EC=CF=AF=$\sqrt{O{A}^{2}+O{E}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$，
∴菱形的周长为8$\sqrt{5}$，
故答案为8$\sqrt{5}$．

点评 本题考查正方形的性质、菱形的判定和性质、勾股定理等知识，解题的关键是灵活运用菱形的判定和性质解决问题，属于中考常考题型．