题目内容
 如图,∠1=88°,∠2=88°,∠3=50°,求∠4.
如图,∠1=88°,∠2=88°,∠3=50°,求∠4.考点:平行线的判定与性质
专题:
分析:结合对顶角相等可先证明EF∥CD,再由平行线的性质可得∠3+∠4=180°,可求得∠4.
解答:解:
∵∠1=∠2=88°,
∴CD∥EF,
∴∠3+∠4=180°,
∴∠4=180°-∠3=180°-50°=130°.
∵∠1=∠2=88°,
∴CD∥EF,
∴∠3+∠4=180°,
∴∠4=180°-∠3=180°-50°=130°.
点评:本题主要考查平行线的性质和性质,掌握平行线的性质和判定是解题的关键,即①两直线平行?同位角相等,②两直线平行?内错角相等,③两直线平行?同旁内角互补,④a∥b,b∥c?a∥c.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列运算中,正确的是( )
| A、x3+x3=2x6 |
| B、(a+b)2=a2+b2 |
| C、(x2)3=x5 |
| D、x3•x3=x6 |
 小明从正面观察如图所示的两个物体,其中所看到的图形是( )
小明从正面观察如图所示的两个物体,其中所看到的图形是( )A、 |
B、 |
C、 |
D、 |
绝对值相等的两个数一定( )
| A、相等 | B、都是0 |
| C、互为相反数 | D、相等或互为相反数 |
 如图,AB垂直平分CD,若AC=1.6cm,BC=2.3cm,则四边形ABCD的周长是( )cm.
如图,AB垂直平分CD,若AC=1.6cm,BC=2.3cm,则四边形ABCD的周长是( )cm.| A、3.9 | B、7.8 |
| C、4 | D、4.6 |
下面从左边到右边的变形是因式分解的是( )
| A、(x+3)(x-3)=x2-9 | ||||||
| B、x2-4+3x=(x-2)(x+2)+3x | ||||||
C、x2+
| ||||||
D、x2-
|
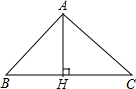 如图,△ABC中,AH是高,已知△ABC的面积为6,且BC2=2AH2+BH2+HC2,
如图,△ABC中,AH是高,已知△ABC的面积为6,且BC2=2AH2+BH2+HC2,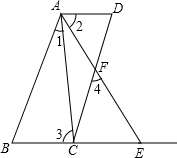 如图AB∥CD.∠1=∠2,∠3=∠4,试说明AD∥BE.
如图AB∥CD.∠1=∠2,∠3=∠4,试说明AD∥BE.