题目内容
若两个相似三角形的相似比为2:3,面积差是30,则它们的面积和为( )
| A、60 | B、78 |
| C、128 | D、150 |
考点:相似三角形的性质
专题:
分析:先根据相似三角形的性质求出其面积的比,再设较小的三角形的面积为4x,则较大的三角形的面积为9x,由它们面积的差是30即可求出x的值,进而得出问题答案.
解答:解:∵两个相似三角形的相似比为2:3,
∴其面积的比等于4:9,
设较小的三角形的面积为4x,则较大的三角形的面积为9x,
∵它们面积的差是30,
∴9x-4x=5x=30,解得x=6,
∴较大三角形的面积=9×6=54,较小的三角形面积=4×6=24,
∴它们的面积和为78,
故选B.
∴其面积的比等于4:9,
设较小的三角形的面积为4x,则较大的三角形的面积为9x,
∵它们面积的差是30,
∴9x-4x=5x=30,解得x=6,
∴较大三角形的面积=9×6=54,较小的三角形面积=4×6=24,
∴它们的面积和为78,
故选B.
点评:本题考查对相似三角形性质的理解.(1)相似三角形周长的比等于相似比;(2)相似三角形面积的比等于相似比的平方;(3)相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列说法正确的是( )
| A、两名同学5次平均分相同,则方差较大的同学成绩更稳定 |
| B、一组数据3,4,4,6,8,5的众数为4 |
| C、必然事件的概率是100%,随机事件的概率是50% |
| D、了解全国每天丢弃的塑料袋的数量,应适合普查的方法 |
若若2×4n×8n=211,则n等于( )
| A、7 | B、4 | C、2 | D、6 |
 小明从正面观察如图所示的两个物体,其中所看到的图形是( )
小明从正面观察如图所示的两个物体,其中所看到的图形是( )A、 |
B、 |
C、 |
D、 |
 如图,AB垂直平分CD,若AC=1.6cm,BC=2.3cm,则四边形ABCD的周长是( )cm.
如图,AB垂直平分CD,若AC=1.6cm,BC=2.3cm,则四边形ABCD的周长是( )cm.| A、3.9 | B、7.8 |
| C、4 | D、4.6 |
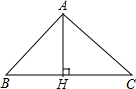 如图,△ABC中,AH是高,已知△ABC的面积为6,且BC2=2AH2+BH2+HC2,
如图,△ABC中,AH是高,已知△ABC的面积为6,且BC2=2AH2+BH2+HC2,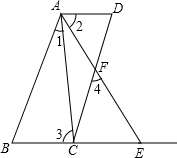 如图AB∥CD.∠1=∠2,∠3=∠4,试说明AD∥BE.
如图AB∥CD.∠1=∠2,∠3=∠4,试说明AD∥BE.