题目内容
3. 如图,在正方形ABCD中,点M,N分别是BC,CD边上的点,连接AM,BN,若BM=CN.
如图,在正方形ABCD中,点M,N分别是BC,CD边上的点,连接AM,BN,若BM=CN.(1)求证:AM⊥BN;
(2)将线段AM绕M顺时针旋转90°得到线段ME,连接NE,试说明:四边形BMEN是平行四边形;
(3)将△ABM绕A逆时针旋转90°得到△ADF,连接EF,当$\frac{BM}{BC}$=$\frac{1}{n}$时,请求出$\frac{{S}_{四边形ABCD}}{{S}_{四边形AMEF}}$的值.
分析 (1)只需证明△ABM≌△BCN即可;
(2)由(1)可知AM=BN且AM⊥BN,而ME是由AM绕点M顺时针旋转90度得到,于是可得ME与BN平行且相等,结论显然;
(3)易证AMEF为正方形,从而问题转化为求两个正方形的边长之比,由于已经知道BM与BC之比,设BM=a,则由勾股定理易求AM.
解答 解:(1)∵ABCD是正方形,
∴AB=BC,∠B=∠C=90°,
在△ABM和△BCN中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABM=∠BCN}\\{BM=CN}\end{array}\right.$
∴△ABM≌△BCN(SAS),
∴∠BAM=∠CBN,
∵∠BAM+∠BMA=90°,
∴∠CBN+∠BMA=90°,
∴AM⊥BN;
(2)∵将线段AM绕M顺时针旋转90°得到线段ME,
∴ME=AM,ME⊥AM,
∵△ABM≌△BCN,
∴AM=BN,
∵AM⊥BN,
∴BN=ME,且BN∥ME,
∴四边形BMEN是平行四边形;
(3)∵将线段AM绕M顺时针旋转90°得到线段ME,将△ABM绕A逆时针旋转90°得到△ADF,
∴∠MAF=∠AME=90°,AF=ME=AM
∴AF∥ME,
∴AMEF是平行四边形,
∴AMEF是正方形,
∵$\frac{BM}{BC}=\frac{1}{n}$,可以设BM=a,AB=na,
在直角三角形ABM中,AM=$\sqrt{{a}^{2}+(na)^{2}}=\sqrt{{n}^{2}+1}a$,
∴$\frac{S四边形ABCD}{S四边形AMEF}$=$\frac{A{B}^{2}}{A{M}^{2}}=\frac{{n}^{2}}{{n}^{2}+1}$.
点评 本题为四边形综合题,主要考查了正方形的判定与基本性质、全等三角形的判定与性质、平行四边形的判定与性质、旋转变换的性质、勾股定理等重要知识点,难度不大.本题虽然简单,但其所包含的基本模型却是很多题的原型,熟练掌握有助于解决相关的较难题目.

| A. | 9 | B. | -9 | C. | $\frac{1}{9\;}$ | D. | $-\frac{1}{9\;}$ |
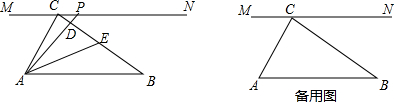
 如图,O是直线AB上一点,∠AOC=∠BOD,射线OE平分∠BOC,∠EOD=42°,求∠EOC的大小.
如图,O是直线AB上一点,∠AOC=∠BOD,射线OE平分∠BOC,∠EOD=42°,求∠EOC的大小.
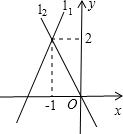 直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k2x<k1x+b的解集为x>-1.
直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k2x<k1x+b的解集为x>-1.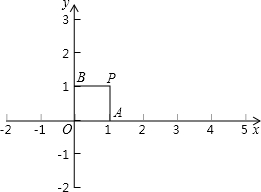 如图,在平面直角坐标系xOy中,已知P(1,1).
如图,在平面直角坐标系xOy中,已知P(1,1).