题目内容
1.已知关于x、y的方程组$\left\{\begin{array}{l}{x+y=7a+6}\\{x-2y=4a-3}\end{array}\right.$的解满足0<x<y,求a的取值范围.分析 首先解方程组,利用a表示出x和y,然后根据0<x<y列不等式组求解.
解答 解:解方程组$\left\{\begin{array}{l}{x+y=7a+6}\\{x-2y=4a-3}\end{array}\right.$
得:$\left\{\begin{array}{l}{x=6a+3}\\{y=a+3}\end{array}\right.$,
根据题意得:$\left\{\begin{array}{l}{6a+3>0}\\{6a+3<a+3}\end{array}\right.$,
解得:-$\frac{1}{2}$<a<0
点评 本题考查了一元一次不等式组的解法:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
相关题目
9.方程3x-6=0的解是( )
| A. | x=3 | B. | x=-3 | C. | x=2 | D. | x=-2 |
6.浙江卫视《中国好声音》总决赛,全国有7100人通过电视收看,这个数据用科学记数法表示为( )
| A. | 71×102 | B. | 7.1×102 | C. | 7.1×103 | D. | 0.71×104 |
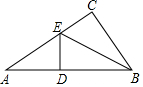 如图所示,在△ABC中,∠C=90°,BE平分∠ABC,ED⊥AB于D,若AC=6cm,则AE+DE=6cm.
如图所示,在△ABC中,∠C=90°,BE平分∠ABC,ED⊥AB于D,若AC=6cm,则AE+DE=6cm. 如图所示,一个四棱柱的底面是一个边长为10cm的正方形,它的高变化时,棱柱的体积也随着变化.
如图所示,一个四棱柱的底面是一个边长为10cm的正方形,它的高变化时,棱柱的体积也随着变化.