题目内容
 已知,如图,在平行四边形ABCD中,DA=DB,E、F分别为AB、BC的中点,连接EF交BD于G.猜想线段DF与EG的数量关系.
已知,如图,在平行四边形ABCD中,DA=DB,E、F分别为AB、BC的中点,连接EF交BD于G.猜想线段DF与EG的数量关系.考点:平行四边形的性质
专题:
分析:作BD的中点H,连接EH、HF,延长DF交AB的延长线于点I,则四边形EBFH是平行四边形,然后证明△BIF≌△CDF,则DF=FI,△DEI是直角三角形,根据直角三角形斜边上的中线等于斜边上的一半求解.
解答:解: 作BD的中点H,连接EH、HF,延长DF交AB的延长线于点I.
作BD的中点H,连接EH、HF,延长DF交AB的延长线于点I.
∵H、F是BD和BC的中点,及HF是△BCD的中位线,
∴HF∥CD,
又∵平行四边形ABCD中,AB∥CD,
∴HF∥AB,
同理,EH∥BC,
∴四边形EBFH是平行四边形.
∴EG=GF=
EF,∠C=∠FBI,
在△BIF和△CDF中,
,
∴△BIF≌△CDF(SAS),
∴DF=FI.
∵DA=DB,E是AB的中点,
∴DE⊥AB,及△DEI是直角三角形,
∴EF=
DI=DF=2EG,
∴DF=2EG.
 作BD的中点H,连接EH、HF,延长DF交AB的延长线于点I.
作BD的中点H,连接EH、HF,延长DF交AB的延长线于点I.∵H、F是BD和BC的中点,及HF是△BCD的中位线,
∴HF∥CD,
又∵平行四边形ABCD中,AB∥CD,
∴HF∥AB,
同理,EH∥BC,
∴四边形EBFH是平行四边形.
∴EG=GF=
| 1 |
| 2 |
在△BIF和△CDF中,
|
∴△BIF≌△CDF(SAS),
∴DF=FI.
∵DA=DB,E是AB的中点,
∴DE⊥AB,及△DEI是直角三角形,
∴EF=
| 1 |
| 2 |
∴DF=2EG.
点评:本题考查了平行四边形的性质以及等腰三角形的性质:三线合一定理,正确作出辅助线是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,
如图,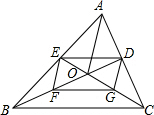 已知E,D,F,G分别是AB,AC,BO,CO的中点,当AB=AC时,证明:四边形DEFG为矩形.
已知E,D,F,G分别是AB,AC,BO,CO的中点,当AB=AC时,证明:四边形DEFG为矩形. 如图:
如图: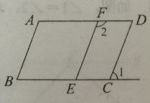 如图,∠2+∠D=180°,∠1=∠B,求证:AB∥EF.
如图,∠2+∠D=180°,∠1=∠B,求证:AB∥EF.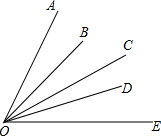 如图所示,五条射线OA、OB、OC、OD、OE组成的图形中共有几个角(小于90°)?如果从O点引出n条射线(最大角为锐角),能有多少个角(小于90°)?你能找出规律吗?
如图所示,五条射线OA、OB、OC、OD、OE组成的图形中共有几个角(小于90°)?如果从O点引出n条射线(最大角为锐角),能有多少个角(小于90°)?你能找出规律吗?