��Ŀ����
�ۺ���̽��
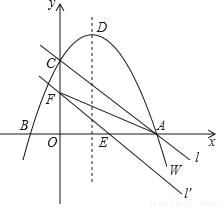
��ͼ����ƽ��ֱ������ϵxOy�У�������W�ĺ�������ʽΪy=��x2+2x+3��������W��x�ύ��A��B���㣨��A�ڵ�B���Ҳࣩ����y�ύ�ڵ�C�����Ķ���ΪD��ֱ��l����A��C���㣮
��1�����A��B��C��D�����꣮
��2����ֱ��l����ƽ��m����λ����Ӧ��ֱ��Ϊl�䣮
����ֱ��l����x��������ύ�ڵ�E����y��������ύ�ڵ�F����AEF�����ΪS����S����m�ĺ�����ϵʽ����д���Ա���m��ȡֵ��Χ��
����m��ֵΪ����ʱ��S��ֵ������ֵΪ���٣�
��3������������WҲ����ƽ��m��λ��������ƽ��1����λ��ʹƽ�ƺ�õ��Ķ��κ���ͼ��Ķ���P���ڡ�AOC���ڲ�����������AOC�ı߽磩����ֱ��д��m��ȡֵ��Χ��
��ϰ��ϵ�д�
�����Ŀ
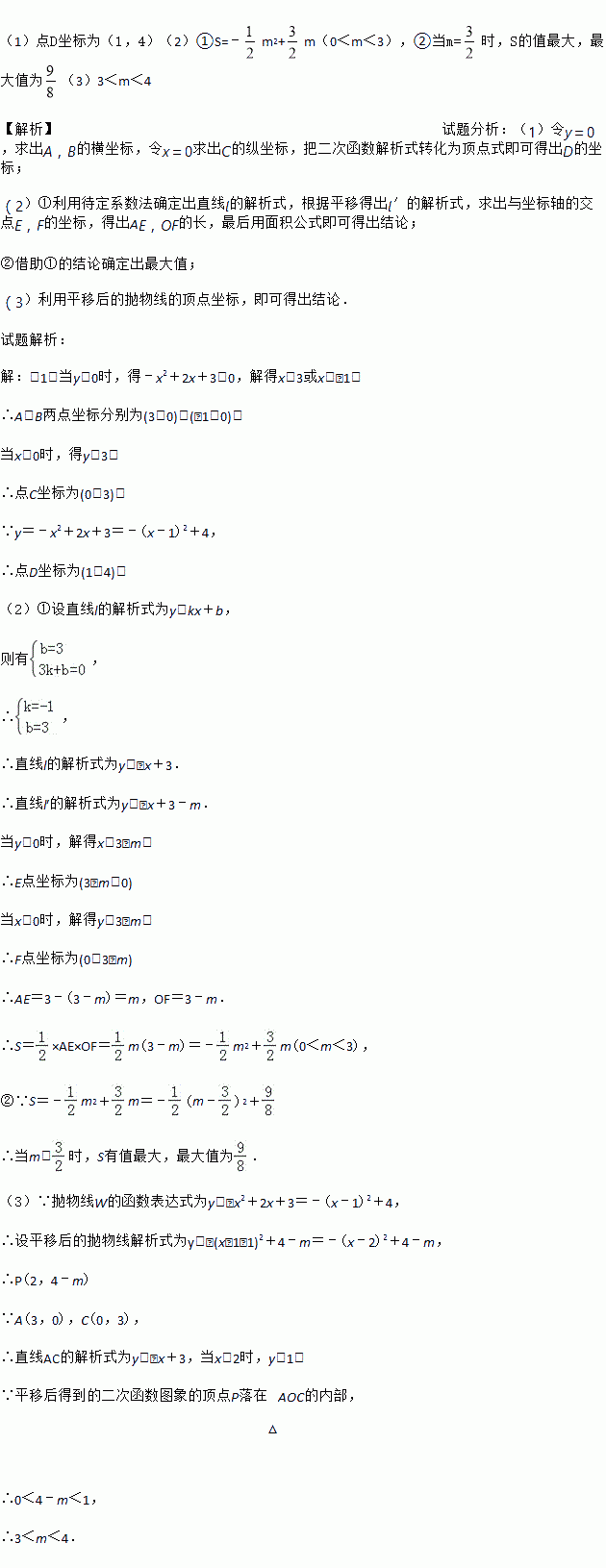

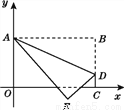
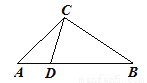
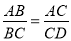 B. ��ADC����ACB
B. ��ADC����ACB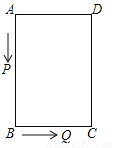
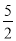 B. 4 C. 5 D. 6
B. 4 C. 5 D. 6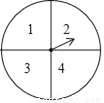
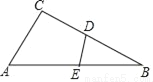
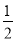 BC C. CD��
BC C. CD��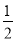 AB��BD D. CD��AD��BC
AB��BD D. CD��AD��BC