题目内容
20.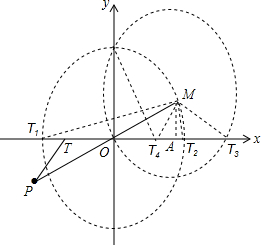 如图,在直角坐标系中,已知P(-2,-1),点T(t,0)是x轴上的一个动点.
如图,在直角坐标系中,已知P(-2,-1),点T(t,0)是x轴上的一个动点.(1)求点P关于原点的对称点M的坐标.
(2)已知点N(0,2)为y轴上的一点,求经过P、M、N三点的抛物线的解析式,并求出该抛物线的顶点坐标.
(3)点T在运动过程中,是否存在某个时刻使△MTO为等腰三角形?若存在,求出点T的坐标.若不存在,请说明理由.
分析 (1)关于原点对称的两个点的横、纵坐标均互为相反数;
(2)设经过P、M、N三点的抛物线的解析式为y=ax2+bx+c(a≠0).把点P、M、N三点的坐标分别代入函数解析式,联立方程组并解答;
(3)分三种情况进行解答:①当OT=OM时,以点O为圆心,以OM为半径画圆,交x轴于两点:T1、T2;
②当OM=MT时,以点M为圆心,以OM为半径画圆,交x轴于两点:O(不合题意)、T3;
③当OM为等腰三角形的底边时,作OM的垂直平分线,交x轴于一点:T4.
结合点的坐标与图形的性质以及函数图象上点的坐标特征进行解答.
解答  解:(1)点P(-2,-1)关于原点的对称点M的坐标为(2,1);
解:(1)点P(-2,-1)关于原点的对称点M的坐标为(2,1);
(2)设经过P、M、N三点的抛物线的解析式为y=ax2+bx+c(a≠0).把P(-2,-1)、M(2,1)、N(0,2)代入,得
$\left\{\begin{array}{l}{4a-2b+c=-1}\\{4a+2b+c=1}\\{c=2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=\frac{1}{2}}\\{c=2}\end{array}\right.$,
∴经过P、M、N三点的抛物线的解析式为y=-$\frac{1}{2}$x2+$\frac{1}{2}$x+2.
又∵y=-$\frac{1}{2}$x2+$\frac{1}{2}$x+2=-$\frac{1}{2}$(x-$\frac{1}{2}$)2+$\frac{17}{8}$,
∴抛物线的顶点坐标为:($\frac{1}{2}$,$\frac{17}{8}$);
(3)∵M(2,1),
∴OM=$\sqrt{5}$,
①当OT=OM时,以点O为圆心,以OM为半径画圆,交x轴于两点:T1、T2
∴OT1=OT2=OM=$\sqrt{5}$,
∴T1(-$\sqrt{5}$,0);T2($\sqrt{5}$,0);
②当OM=MT时,以点M为圆心,以OM为半径画圆,交x轴于两点:O(不合题意)、T3
∵M(2,1),且OM=MT3,
∴OT3=4,
∴T3(4,0);
③当OM为等腰三角形的底边时,作OM的垂直平分线,交x轴于一点:T4,
设OT4的长为a,
∵M(2,1),
∴AT4=2-a,MA=1,
∴在Rt△MAT4中,MT42=(2-a)2+12,
∴(2-a)2+12=a2,
解得:a=$\frac{5}{4}$,
∴T4($\frac{5}{4}$,0).
总之,符合条件的T点存在,共有四个:T1(-$\sqrt{5}$,0);T2($\sqrt{5}$,0)、T3(4,0)、T4($\frac{5}{4}$,0).
点评 本题综合考查了待定系数法求二次函数解析式,二次函数解析式的三种形式,二次函数图象上点的坐标特征以及等腰三角形的判定与性质.解答(3)题时,没有明确等腰三角形的底边时,一定要分类讨论,以防漏解.另外,在利用待定系数法求二次函数解析式时,要根据题中已知条件选择二次函数解析式的形式.

| A. | 2,3,4 | B. | 4,5,7 | C. | 0.5,1.2,1.3 | D. | 12,36,39 |
| A. | 经过一个点画一条直线 | B. | 两点之间,线段最短 | ||
| C. | 同角的余角相等 | D. | 对顶角不相等 |
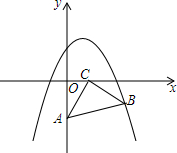 在平面直角坐标系中,将一块等腰直角三角板ABC放在第四象限,一条直角边靠在两坐标轴上,且有点A(0,-2),点C(1,0),抛物线y=ax2-ax+2 经过点B.
在平面直角坐标系中,将一块等腰直角三角板ABC放在第四象限,一条直角边靠在两坐标轴上,且有点A(0,-2),点C(1,0),抛物线y=ax2-ax+2 经过点B.
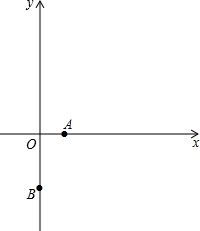 如图,抛物线y=-x2+5x+c经过点A(1,0),与y轴交于点B.
如图,抛物线y=-x2+5x+c经过点A(1,0),与y轴交于点B.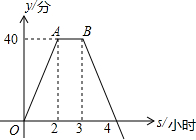 为保护未成年人身心健康,某热门网络游戏实施未成年人防沉迷系统,下图是这种网络游戏的积分增加值(游戏结束时的积分-游戏开始时的积分)y与连续上网时间xh的变化如图所示
为保护未成年人身心健康,某热门网络游戏实施未成年人防沉迷系统,下图是这种网络游戏的积分增加值(游戏结束时的积分-游戏开始时的积分)y与连续上网时间xh的变化如图所示