题目内容
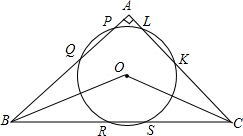 如图,在△ABC中,∠A为直角,⊙O与三角形三边交于点P、Q、R、S、K、L,若PQ=RS=KL,求∠BOC的大小.
如图,在△ABC中,∠A为直角,⊙O与三角形三边交于点P、Q、R、S、K、L,若PQ=RS=KL,求∠BOC的大小.考点:垂径定理,角平分线的性质
专题:
分析:先根据三角形内角和定理得出∠ABC+∠ACB的度数,过点O作OE⊥AB,OF⊥AC,OG⊥BC,再根据PQ=RS=KL可知OE=OF=OG,故OB,OC分别是∠ABC与∠ACB的平分线,故可得出∠OCG=
ACB,∠OBG=
∠ABC,再由三角形内角和定理即可得出结论.
| 1 |
| 2 |
| 1 |
| 2 |
解答: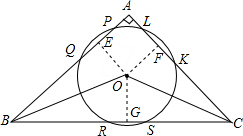 解:∵∠A=90°
解:∵∠A=90°
∴∠ABC+∠ACB=90°.
过点O作OE⊥AB,OF⊥AC,OG⊥BC,
∵PQ=RS=KL,
∴EE=OF=OG,
∴OB,OC分别是∠ABC与∠ACB的平分线,
∴∠OCG=
ACB,∠OBG=
∠ABC,
∴∠BOC=180°-∠OCG-∠=∠ACB,∠OBG,
∵∠BOC=180°-(∠OCG+∠OBG)=180°-
(∠ABC+∠ACB)=180°-20°-20=140.
 解:∵∠A=90°
解:∵∠A=90°∴∠ABC+∠ACB=90°.
过点O作OE⊥AB,OF⊥AC,OG⊥BC,
∵PQ=RS=KL,
∴EE=OF=OG,
∴OB,OC分别是∠ABC与∠ACB的平分线,
∴∠OCG=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOC=180°-∠OCG-∠=∠ACB,∠OBG,
∵∠BOC=180°-(∠OCG+∠OBG)=180°-
| 1 |
| 2 |
点评:本题考查的是垂径定理,熟知平分弦的直径平分这条弦,并且平分弦所对的两条弧是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若(a-2)2+|b+3|=0,则(a+b)2007的值是( )
| A、-1 | B、1 | C、0 | D、2007 |
 如图,矩形ABCD中对角线交于点O,DE平分∠ADC交BC于E,∠AOB=60°,求∠COE的度数.(提示:说明EC=OC)
如图,矩形ABCD中对角线交于点O,DE平分∠ADC交BC于E,∠AOB=60°,求∠COE的度数.(提示:说明EC=OC) 如图,AB为⊙O的直径,点D是
如图,AB为⊙O的直径,点D是
 如图,是某个几何体从不同方向看到的形状图(视图),这个几何体的表面能展开成下面的哪个平面图形?( )
如图,是某个几何体从不同方向看到的形状图(视图),这个几何体的表面能展开成下面的哪个平面图形?( )



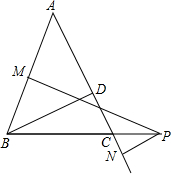 如图,在△ABC中,AB=AC,BD是AC边上的高,P为BC延长线上的一点,PM⊥AB,PN⊥AC,垂足分别是M,N,试问PM、PN与BD之间有何关系?
如图,在△ABC中,AB=AC,BD是AC边上的高,P为BC延长线上的一点,PM⊥AB,PN⊥AC,垂足分别是M,N,试问PM、PN与BD之间有何关系?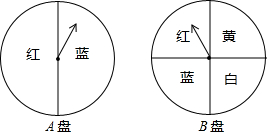 依次转动如图所示的两个转盘进行“配紫色”(红色与蓝色可配得紫色)游戏,每个转盘都被分成面积相等的几个扇形,请你用画树状图或列表的方法,求配得紫色的概率.
依次转动如图所示的两个转盘进行“配紫色”(红色与蓝色可配得紫色)游戏,每个转盘都被分成面积相等的几个扇形,请你用画树状图或列表的方法,求配得紫色的概率. 如图,在⊙O的弦AB的长等于⊙O的半径,求∠ACB的度数.
如图,在⊙O的弦AB的长等于⊙O的半径,求∠ACB的度数.