Question

10．一副量角器与一块含30°锐角的三角板如图所示放置，三角板的顶点C恰好落在量角器的直径MN上，顶点A，B恰好落在量角器的圆弧上，且AB∥MN．若AB=8，则量角器的直径MN=4$\sqrt{7}$．

Answer 1

分析 作CD⊥AB于点D，取圆心O，连接OA，作OE⊥AB于点E，首先求得CD的长，即OE的长，在直角△AOE中，利用勾股定理求得半径OA的长，则MN即可求解．

解答 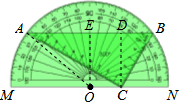解：作CD⊥AB于点D，取圆心O，连接OA，作OE⊥AB于点E．
在直角△ABC中，∠A=30°，则BC=$\frac{1}{2}$AB=4，
在直角△BCD中，∠B=90°-∠A=60°，
∴CD=BC•sinB=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$，
∴OE=CD=2$\sqrt{3}$，
在△AOE中，AE=$\frac{1}{2}$AB=4，
则OA=$\sqrt{A{E}^{2}+O{E}^{2}}$=$\sqrt{16+12}$=2$\sqrt{7}$，
则MN=2OA=4$\sqrt{7}$．
故答案是：4$\sqrt{7}$．

点评 本题考查了垂径定理的应用，在半径或直径、弦长以及弦心距之间的计算中，常用的方法是转化为解直角三角形．