题目内容
13.给定直线l:y=kx,抛物线C:y=ax2+x+1,l与C相交于A,B两点,其中A为C的顶点,B与A关于原点对称,求a的值.分析 根据两交点关于原点对称,可得k的值,根据抛物线的顶点坐标在y=x上,可得关于a的方程,根据解方程,可得答案.
解答 解:∵l:y=kx,C:y=ax2+bx+1,当b=1时有A,B两交点,
∴A,B两点的横坐标满足kx=ax2+x+1,即ax2+(1-k)x+1=0.
∵B与A关于原点对称,
∴0=xA+xB=$\frac{k-1}{a}$,
∴k=1.
∵y=ax2+x+1=a(x+$\frac{1}{2a}$)2+1-$\frac{1}{4a}$,
∴顶点(-$\frac{1}{2a}$,1-$\frac{1}{4a}$)在y=x上,
∴-$\frac{1}{2a}$=1-$\frac{1}{4a}$,
解得a=-$\frac{1}{4}$.
点评 本题考查了二次函数的性质,利用图象的交点坐标得出k的值是解题关键,又利用顶点坐标在直线y=x上得出关于a的方程.

练习册系列答案
相关题目
3.下列实数是无理数的是( )
| A. | -1 | B. | 0 | C. | 3.14 | D. | $\sqrt{5}$ |
3.下列表格给出了第28届奥运会上获得金牌前四名的国家的奖牌情况,请制作扇形统计图反映以下四个国家获得奖牌总数的情况.
| 国家 | 金牌 | 银牌 | 铜牌 |
| 美国 | 35 | 39 | 29 |
| 中国 | 32 | 17 | 14 |
| 俄罗斯 | 27 | 27 | 38 |
| 澳大利亚 | 17 | 16 | 16 |
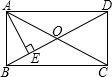 如图,矩形ABCD中,∠DAE:∠BAE=3:1,AE⊥BD,则∠EAC等于45°.
如图,矩形ABCD中,∠DAE:∠BAE=3:1,AE⊥BD,则∠EAC等于45°.