Question

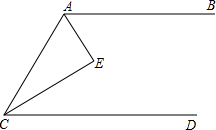如图，AB∥CD，AE、CE分别平分∠BAC、∠ACD，则∠AEC的大小是（　　）

• A、90°
• B、80°
• C、70°
• D、60°

Answer 1

考点：平行线的性质

专题：

分析：根据平行线的性质得∠BAC+∠DCA=180°，再根据角平分线的定义得∠EAC=

1

2

∠BAC，∠ECA=

1

2

∠DCA，则∠EAC+∠ECA=90°，然后根据三角形内角和定理可计算出∠AEC．

解答：解：∵AB∥CD，
∴∠BAC+∠DCA=180°，
∵AE，CE分别平分∠BAC，∠ACD，
∴∠EAC=

1

2

∠BAC，∠ECA=

1

2

∠DCA，
∴∠EAC+∠ECA=

1

2

（∠BAC+∠DCA）=90°，
∴∠AEC=90°．
故选A．

点评：本题考查的是平行线的性质，熟知两直线平行，同旁内角互补是解答此题的关键．